Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì ABCD.A1B1C1D1 là hình hộp chữ nhật nên DCC1D1 và CBB1C1 là hình chữ nhật.
=> CC1 = BB1 = 3cm

Bài 1:
Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
DO đó: F là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình
=>EF//BC
hay BEFC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BEFC là hình thang cân

Thể tính hình hộp chữ nhật là:
\(V=3\sqrt{2}.4\sqrt{2}.5=120\left(cm^3\right)\)

Áp dụng định lý Pi - ta - go, ta có :
\(AB=\sqrt{CA^2+CB^2}=\sqrt{3^2+4^2}=\sqrt{25}=5cm\)
Áp dụng định lý ' Trong tam giác vuông , trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền ' ở đây là
\(CM=\frac{.AB}{2}=\frac{5}{2}=2,5cm\)
A C B 3cm 4cm

a, \(\frac{2x}{x+1}+\frac{18}{x^2+2x-3}=\frac{2x-5}{x+3}\)
\(\Leftrightarrow\frac{2x}{x+1}+\frac{18}{\left(x+3\right)\left(x-1\right)}=\frac{2x-5}{x+3}\)
\(\Leftrightarrow\frac{2x\left(x-1\right)\left(x+3\right)}{\left(x+1\right)\left(x-1\right)\left(x+3\right)}+\frac{18\left(x+1\right)}{\left(x+3\right)\left(x-1\right)\left(x+1\right)}=\frac{\left(2x-5\right)\left(x+1\right)\left(x-1\right)}{\left(x-1\right)\left(x+3\right)\left(x+1\right)}\)
\(\Leftrightarrow2x\left(x-1\right)\left(x+3\right)+18\left(x+1\right)=\left(2x+5\right)\left(x+1\right)\left(x-1\right)\)
\(\Leftrightarrow2x^3+4x^2-6x+18x+18=2x^3-2x+5x^2-5\)
\(\Leftrightarrow-x^2+14x+23=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=7-6\sqrt{2}\\x=7+6\sqrt{2}\end{cases}}\)
Vậy...
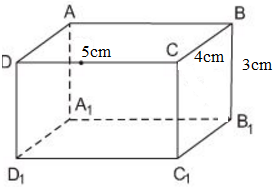
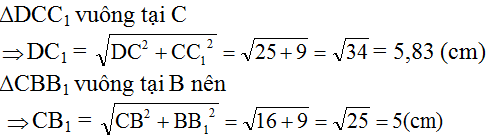
Vì ABCD.A1B1C1D1 là hình hộp chữ nhật
⇒ DCC1D1 và CBB1C1 là hình chữ nhật.
⇒ CC1 = BB1 = 3cm
ΔDCC1 vuông tại C, áp dụng định lí Py-ta–go ta có:
DC12 = DC2 + CC12
ΔCBB1 vuông tại B, áp dụng định lí Py–ta-go ta có:
CB12= CB2 + BB12