Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đạo hàm : y ' = 3 + m ( cos x - sin x ) = 3 + m 2 cos ( x + π 4 )
Hàm số đồng biến trên R khi y’ ≥ 0 với mọi x
⇔ M i n ℝ y ' ≥ 0 ⇔ 3 - m 2 ≥ 0 ⇔ m ≤ 3 2 → m ∈ ℤ m = 0 ; m = ± 1 ; m = ± 2 .
Vậy có 2 giá trị nguyên dương của m thỏa mãn đầu bài.
Chọn D.

+ Tính đạo hàm y ' = cos x + sin x + 2017 2 m .
y ' ≥ 0 ⇔ m ≥ - sin x - cos x 2017 2 = f ( x )
+ Theo bất đẳng thức Bunhiacopxki thì
( - sin x - cos x ) 2 ≤ ( - 1 ) 2 + ( - 1 ) 2 sin 2 x + cos 2 x = 2 - 2 ≤ ( - sin x - cos x ) ≤ 2
Do đó :
- 2 2017 2 ≤ f ( x ) ≤ 2 2017 2
F(x) đạt giá trị lớn nhất là 2 2017 2 = 1 2017 ⇒ m ≥ f ( m a x ) = 1 2017
Chọn C.

Chọn D
Đặt ![]() ,
, ![]() thì
thì ![]() . Ta có:
. Ta có:
![]()
![]()
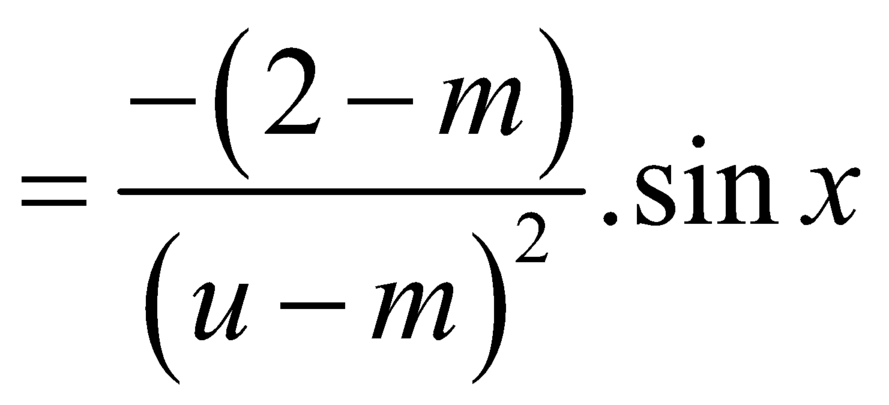 .
.
Vì ![]() nên ycbt
nên ycbt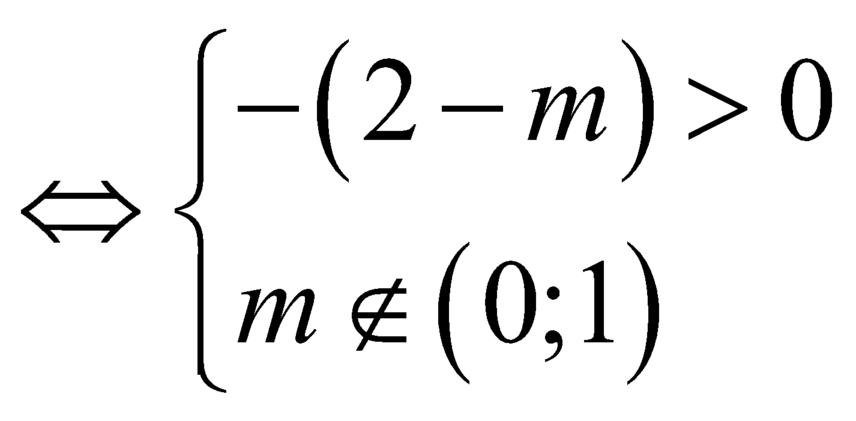 .
.
Đến đây giải được: ![]() .
.
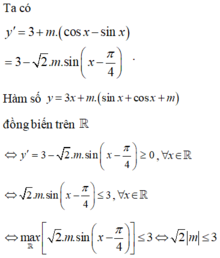
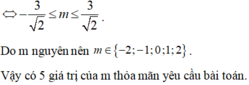
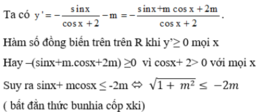
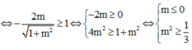
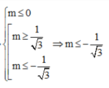
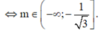
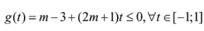
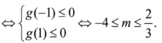
Hàm số \(y=x+m\left(\sin x+\cos x\right)\)đồng biến trên \(R\) khi và chỉ khi:
\(y'=1+m\left(\cos x-\sin x\right)\ge0,\forall x\in R\)
\(\Leftrightarrow\min\limits\left(1+m\left(\cos x-\sin x\right)\right)\ge0,\forall x\in R\)(1)
Trước tiên ta sẽ đi tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: \(g\left(x\right)=\sin x-\cos x\)
Đặt \(t=\sin x+\cos x\Rightarrow2\sin x.\cos x=t^2-1\)
Ta có \(\left(g\left(x\right)\right)^2=\left(\cos x-\sin x\right)^2=2-t^2\le2\Rightarrow-\sqrt{2}\le g\left(x\right)\le\sqrt{2}\)
Do đó\(\left|m\left(\cos x-\sin x\right)\right|=\left|m\right|.\left|\cos x-\sin x\right|\le\left|m\right|\sqrt{2}\)
\(\Rightarrow-\sqrt{2}\left|m\right|\le m\left(\cos x-\sin x\right)\le\sqrt{2}\left|m\right|\)
Do đó (1)\(\Leftrightarrow1-\sqrt{2}\left|m\right|\ge0\Leftrightarrow\dfrac{-1}{\sqrt{2}}\le m\le\dfrac{1}{\sqrt{2}}\)
bạn ơi, có thể nói đoạn dưới rõ hơn được không , mìn cũng không hiểu lắm . cảm ơn bạn nhiều