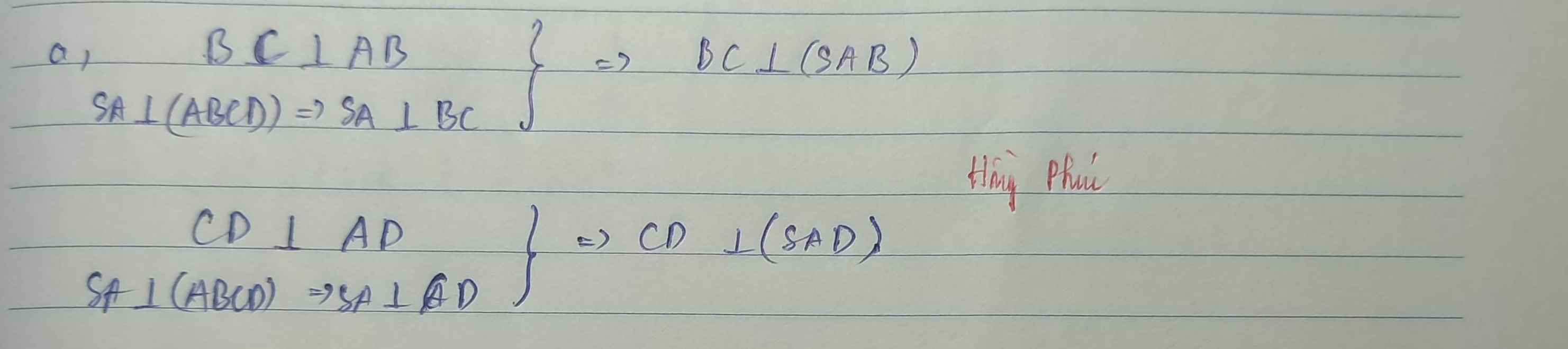K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1
E
14 tháng 12 2021
Câu d có thể liệt kê ra, hoặc làm như sau:
Dễ dàng nhận ra với lần đầu tiên tung ra mặt có số chấm là 1,2,5,6 thì chỉ có 1 khả năng để 2 lần cách nhau 2 chấm là 3,4,3,4
Còn với các chấm 3 và 4 xuất hiện ở lần đầu thì có 2 khả năng tung lần 2 để 2 lần gieo cách nhau 2 chấm
Như vậy n(C) = 4.1 + 2.2 = 8
giúp em câu hình với ạ. Làm ơn
1 tháng 5 2023
3:
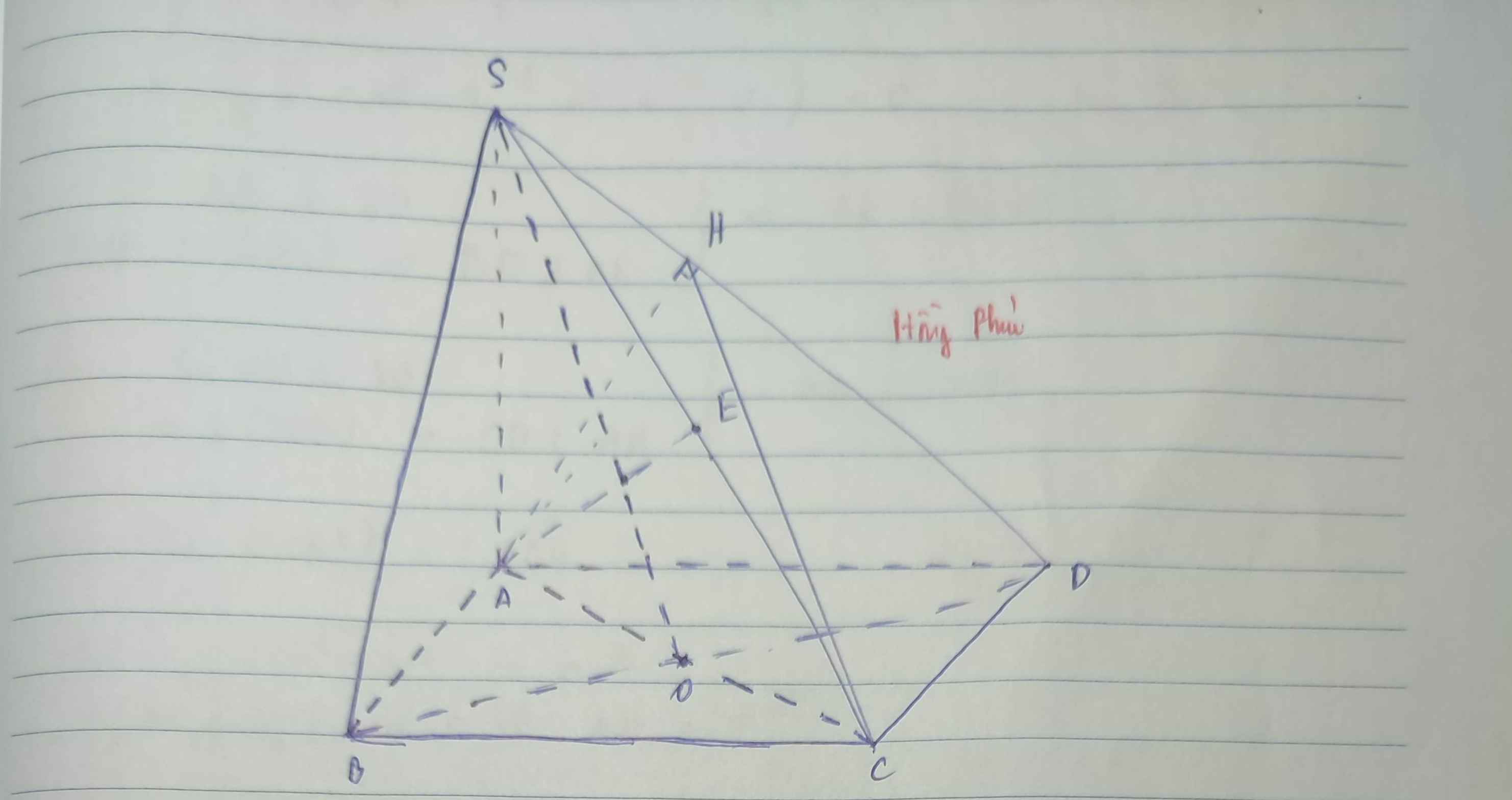
a: BC vuông góc AB
BC vuông góc SI
=>BC vuông góc (SAB)
=>(SAB) vuôg góc (SBC)
CN vuông góc ID
CN vuông góc SI
=>CN vuông góc (SID)
=>(SCN) vuôg góc (SID)
DN
1
DK
5
TB
1
HP
23 tháng 9 2021
j, ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
\(tan\left(\dfrac{\pi}{3}+x\right)-tan\left(\dfrac{\pi}{6}+2x\right)=0\)
\(\Leftrightarrow tan\left(\dfrac{\pi}{3}+x\right)=tan\left(\dfrac{\pi}{6}+2x\right)\)
\(\Leftrightarrow\dfrac{\pi}{3}+x=\dfrac{\pi}{6}+2x+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\left(l\right)\)
\(\Rightarrow\) vô nghiệm.
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
5.
\(AA'\perp\left(A'B'C'D'\right)\) theo t/c lập phương
\(\Rightarrow AA'\perp B'C'\Rightarrow\) góc giữa 2 đường thẳng bằng 90 độ
6.
\(y'=\left(x.cosx\right)'=x'.cosx+\left(cosx\right)'.x=cosx-x.sinx\)
7.
\(y'=-3x^2-5\)
\(y''=-6x\)
8.
\(\lim\limits_{x\rightarrow+\infty}\left(x^3+3x-2\right)=\lim\limits_{x\rightarrow+\infty}x^3\left(1+\dfrac{3}{x}-\dfrac{2}{x^3}\right)=+\infty.1=+\infty\)
14 tháng 6 2023
a: NQ vuông góc MP
NQ vuông góc SM
=>NQ vuông góc (SMP)
b: (SP;MNPQ)=(PS;PM)=góc SPM
tan SPM=SM/MP=căn 3/2
=>góc SPM=51 độ
VT
Vũ Thị Minh Ánh
Giáo viên
18 tháng 12 2022
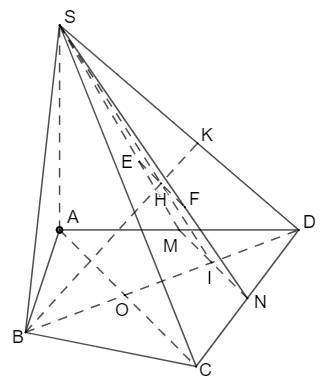
a) Trong (ABCD): Gọi O là giao điểm của AC và BD.
SO là giao tuyến của (SAC) và (SBD).
b) Gọi M là trung điểm của AD, N là trung điểm của CD.
Trong (ABCD) gọi I là giao điểm của BD và MN.
Trong (SMN) gọi H là giao điểm của SI và EF.
Trong (SBD) gọi K là giao điểm của BH và SD.
K là giao của SD với (BEF).
