
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bài 1 : Chứng minh 2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau
bài 2 : cho hình vẽ có góc BAC = 120 độ ; góc ADC = 30 độ và BAC+ACD = 180 độ
a ) tính góc xCD
b ) tính góc BAD
c ) chứng minh AD\(\perp\) AC
( vẽ hình ghi giả thiết kết luật rồi mới làm )
bài 3 : cho tam giác ABC có A1 = A2 . EF//AB ; FI//AE
1/ chứng minh góc A2 bằng góc AEF
2/ chứng minh FI là tia phân giác góc EFC
( vẽ hình ghi giả thiết kết luật rồi làm )

Nếu bạn đánh riêng từng câu ra, có thể mk sẽ giúp đó. Chứ như vậy khó nhìn trả lời lắm bạn ạ.

Ta có:M là trung điểm của BC=>BM=MC
Mà IM=\(\frac{BM}{2}\)(I là trung điểm của BM)
=>IM\(=\frac{MC}{2}\)(1)
Vì IA=IE(gt)
=>CI là đường trung tuyến ứng với cạnh AE của \(\Delta AEC\)(2)
Từ (1),(2)=>M là giao điềm của 3 đường trung tuyến của \(\Delta AEC\)
Vì N là trung điểm của EC(gt)
=>AN là đường trung tuyến ứng với cạnh EC của \(\Delta AEC\)
Xét \(\Delta AEC\)có:
AN là đường trung tuyến ứng với cạnh EC
M là giao điểm của 3 đường trung tuyến
=>A,M,N thẳng hàng
Mình ko biết vẽ hình ở đâu nên ko vẽ mà chỉ trình bày thôi.
Bài giải
*Ta có:
+ M là td của BC (gt) => MB=MC(t/c)
+ I là td của BM (gt) => IM= IB(t/c)
mà MB=MC(cmt) => IM=IB=1/2 MC
=> M là trọng tâm ( t/c trọng tâm )
*Xét tam giác AEC có :
I là td của AE (gt) =>CI là trung tuyến
N là td của EC (gt) =>AN là trung tuyến
mà M là trọng tâm (cmt) => M thuộc AN
=> A,M,N thẳng hàng (dpcm)

Đây là toán nâng cao chuyên đề tìm phương trình nghiệm nguyên, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp đánh giá như sau:
Giải:
20\(^x\) : 14\(^x\) = \(\dfrac{10}{7}\)\(x\) (\(x\) \(\in\) N)
\(\left(\dfrac{20}{14}\right)^x\) = \(\dfrac{10}{7}\)⇒ \(x\)\(\left(\dfrac{10}{7}\right)^x\) = \(\dfrac{10}{7}\)\(x\)
\(x\) = \(\left(\dfrac{10}{7}\right)^x\): \(\dfrac{10}{7}\) ⇒ \(x\) =\(\left(\dfrac{10}{7}\right)^{x-1}\)
Nếu \(x\) = 0 ta có 0 = (\(\dfrac{10}{7}\))-1 = \(\dfrac{7}{10}\) (vô lý)
Nếu \(x\) = 1 ta có: 1 = \(\left(\dfrac{10}{7}\right)^{1-1}\) = 1 (nhận)
Nếu \(x\) > 1 ta có: \(x\) \(\in\) N mà (\(\dfrac{10}{7}\))\(x\) không phải là số tự nhiên nên
\(x\) \(\ne\) (\(\dfrac{10}{7}\))\(x-1\) (loại)
Từ những lập luận trên ta có \(x\) = 1 là số tự nhiên duy nhất thỏa mãn đề bài.
Vậy \(x\) = 1

Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Câu 2
a) Thay y = -2 vào biểu thức đã cho ta được:
2.(-2) + 3 = -1
Vậy giá trị của biểu thức đã cho tại y = -2 là -1
b) Thay x = -5 vào biểu thức đã cho ta được:
2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40
Vậy giá trị của biểu thức đã cho tại x = -5 là 40

quá dễ : cung tên chứ cái j nữa. cung bắn chứ đâu bay dc. còn tên thì bay dc hà

dễ thấy vế trái luôn>0 nên 6x>0=> x>0
x>0, bỏ dấu trị tuyệt đối ra ta đc 4x+10=6x
x=5
chúc bạn học giỏi, ăn Tết đc ngon, hehe -_-
HYC-30/1/2022
Answer:
\(\left|x+1\right|+\left|x+2\right|+\left|x+3\right|+\left|x+4\right|=6x\)
Có \(\left|x+1\right|+\left|x+2\right|+\left|x+3\right|+\left|x+4\right|\ge0\)
\(\Rightarrow6x\ge0\)
\(\Rightarrow x\ge0\)
\(\Rightarrow x+1+x+2+x+3+x+4=6x\)
\(\Rightarrow4x+10=6x\)
\(\Rightarrow2x=10\)
\(\Rightarrow x=5\)
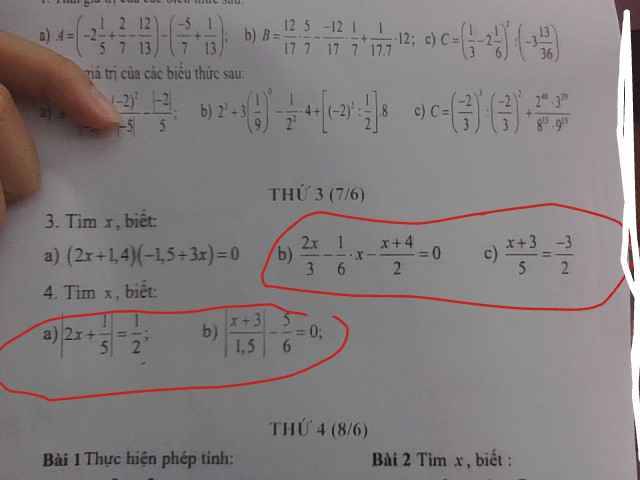 CÁC BẠN LÀM GIÚP MIK BÀI 4 HAY CÒN GỌI LÀ BÀI 2 THỨ 3 ĐC KO
CÁC BẠN LÀM GIÚP MIK BÀI 4 HAY CÒN GỌI LÀ BÀI 2 THỨ 3 ĐC KO

Cách làm bài 4 b giống 4 a là bỏ trị tuyệt đối , bạn có 2 số
đáp số bài 4 b
x = 3/20 hay x = - 7/20