Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. TXĐ: \(D=R\)
Với mọi \(x\in D\Rightarrow x\pm2\pi\in D\)
Đồng thời:
\(y\left(x+2\pi\right)=sin\left(x+2\pi\right)+cos\left(2x+4\pi\right)=sinx+cos2x=y\left(x\right)\)
\(\Rightarrow\) Hàm là hàm tuần hoàn với chu kì \(T=2\pi\)
b. TXĐ: \(D=R\)
Với mọi \(x\in D\Rightarrow x\pm\dfrac{2\pi}{3}\in D\)
\(y\left(x+\dfrac{2\pi}{3}\right)=sin\left(3x+2\pi\right)=sin3x=y\left(x\right)\)
\(\Rightarrow\) Hàm là hàm tuần hoàn với chu kì \(T=\dfrac{2\pi}{3}\)

Đáp án D
Hàm số đã cho tuần hoàn với chu kỳ 2 π và kết hợp với các phương án đề bài thì ta sẽ xét sự biến thiên của hàm số trên (-π/2; 3π/2)
Ta có hàm số y = sin x
* Đồng biến trên khoảng (-π/2; π/2)
* Nghịch biến trên khoảng (π/2; 3π/2)
Từ đây suy ra hàm số y = 1 - sinx
* Nghịch biến trên khoảng (-π/2; π/2)
* Đồng biến trên khoảng (π/2; 3π/2)

Ta có y = 2cos2x – 1 = cos2x, do đó hàm số tuần hoàn với chu kì T = 2π/2 = π.
Vậy đáp án là A.
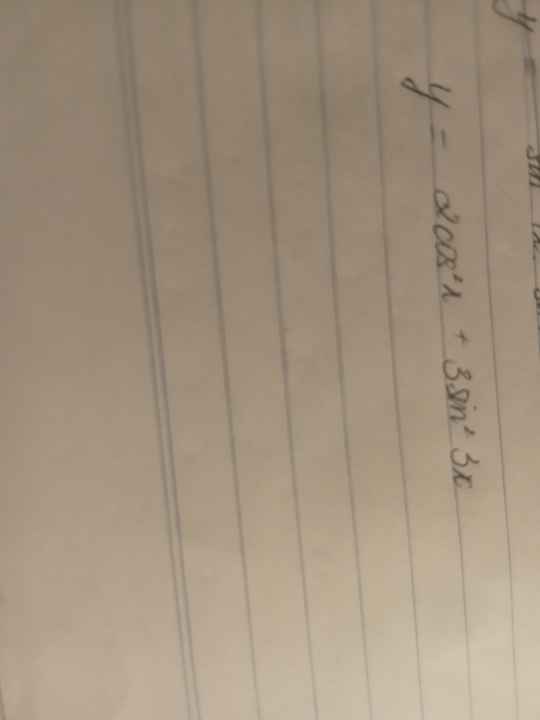



\(y=cos2x-1+\dfrac{3}{2}-\dfrac{3}{2}cos6x=\dfrac{1}{2}+cos2x-\dfrac{3}{2}cos6x\)
Hàm \(f\left(x\right)=cos2x\) có chu kì \(T_1=\dfrac{2\pi}{\left|2\right|}=\pi\)
Hàm \(g\left(x\right)=cos6x\) có chu kì \(T_2=\dfrac{2\pi}{\left|6\right|}=\dfrac{\pi}{3}\)
\(\Rightarrow\) Hàm \(y\) có chu kì \(T=BCNN\left(\pi;\dfrac{\pi}{3}\right)=\pi\)