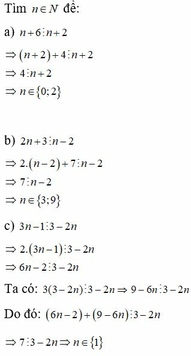K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
3
AH
Akai Haruma
Giáo viên
28 tháng 12 2023
Câu c/
$6n+2\vdots 2n-1$
$3(2n-1)+5\vdots 2n-1$
$\Rightarrow 5\vdots 2n-1$
$\Rightarrow 2n-1\in Ư(5)$
$\Rightarrow 2n-1\in \left\{1; -1; 5; -5\right\}$
$\Rightarrow n\in \left\{1; 0; 3; -2\right\}$
AH
Akai Haruma
Giáo viên
28 tháng 12 2023
Câu a/
$2n-3\vdots n+1$
$2(n+1)-5\vdots n+1$
$5\vdots n+1$
$\Rightarrow n+1\in Ư(5)$
$\Rightarrow n+1\in \left\{1; -1; 5; -5\right\}$
$\Rightarrow n\in \left\{0; -2; 4; -6\right\}$
1 tháng 12 2017
2.a)n^5+1⋮n^3+1
⇒n^2.(n^3+1)-n^2+1⋮n^3+1
⇒1⋮n^3+1
⇒n^3+1ϵƯ(1)={1}
ta có :n^3+1=1
n^3=0
n=0
Vậy n=0
b)n^5+1⋮n^3+1
Vẫn làm y như bài trên nhưng vì nϵZ⇒n=0
Bữa sau giải bài 3 mình buồn ngủ quá!!!!!!!!
NN
3
22 tháng 11 2016
Ưc(2n+1,3n+1)={1}
ƯC(2n+1,2n+3)={1}
ƯC(2n+1,2n+3)={1}
QC
1
10 tháng 4 2022
a: Gọi d=UCLN(2n+1;2n+3)
\(\Leftrightarrow2n+3-2n-1⋮d\)
\(\Leftrightarrow2⋮d\)
mà 2n+1 là số lẻ
nên d=1
=>(2n+1;2n+3)=1
b: Gọi a=UCLN(2n+7;n+3)
\(\Leftrightarrow2n+7-2n-6⋮a\)
=>a=1
=>UCLN(2n+7;n+3)=1
PT
1
PT
1
CM
23 tháng 12 2019
a, n+6 ⋮ n+2 => (n+2)+4 ⋮ n+2
=> 4 ⋮ n+2
=> n ∈ {0;2}
b, 2n+3 ⋮ n - 2
=> 2.(n - 2)+7 ⋮ n - 2
=> 7 ⋮ n - 2
=> n ∈ {3;9}
c, 3n - 1 ⋮ 3 - 2n
=> 2.(3n - 1) ⋮ 3 - 2n
=> 6n - 2 ⋮ 3 - 2n
Ta có: 3(3 - 2n) ⋮ 3 - 2n => 9 - 6n ⋮ 3 - 2n
Do đó: (6n - 2)+(9 - 6n) ⋮ 3 - 2n
=> 7 ⋮ 3 - 2n => n ∈ {1}
12 tháng 8 2018
( Tự tính nhá...các câu na ná nhau... )
\(a)\dfrac{7}{3n-1}\) là số tự nhiên thì 3n - 1 ϵ Ư(7) = \(\left\{\pm1,\pm7\right\}\) .....
\(b)\dfrac{n+5}{n+3}=\dfrac{n+3+2}{n+3}=1+\dfrac{2}{n+3}\)
\(\Rightarrow n+3\inƯ\left(2\right)=\left\{\pm1,\in2\right\}\) .....
\(c)\dfrac{n-3}{n-1}=\dfrac{n-1-2}{n-1}1-\dfrac{2}{n-1}\\ \Rightarrow n-1\inƯ\left(2\right)=\left\{\pm1,\pm2\right\}......\)
9 tháng 8 2022
d: Ta có: 3n+1 chia hết cho n-1
=>3n-3+4 chia hết cho n-1
\(\Leftrightarrow n-1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{2;0;3;-1;5;-3\right\}\)
e: =>5n-5 chia hết cho 5n+1
\(\Leftrightarrow5n+1\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
hay \(n\in\left\{0;-\dfrac{2}{5};\dfrac{1}{5};-\dfrac{3}{5};\dfrac{2}{5};-\dfrac{4}{5};1;-\dfrac{7}{5}\right\}\)
f: =>5n+5-5 chia hết cho n+1
\(\Leftrightarrow n+1\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{0;-2;4;-6\right\}\)
17 tháng 2 2020
a)(2n + 6) ⋮ (2n - 1)
Do đó ta có (2n + 6) = (2n - 1) + 7
Nên 7 ⋮ 2n - 1
Vậy 2n - 1 ∈ Ư(7) = {-1; 1; -7; 7}
Ta có bảng sau :
| 2n - 1 | -1 | 1 | -7 | 7 |
| 2n | 0 | 2 | -6 | 8 |
| n | 0 | 1 | -3 | 4 |
➤ Vậy n ∈ {0; 1; -3; 4}
b)(3n + 7) ⋮ (n - 2)
(3n + 7) ⋮ 3(n - 2)
Do đó ta có (3n + 7) = 3(n - 2) + 13
Nên 13 ⋮ n - 2
Vậy n - 2 ∈ Ư(13) = {-1; 1; -13; 13}
Ta có bảng sau :
| n - 2 | -1 | 1 | -13 | 13 |
| n | 1 | 3 | -11 | 15 |
➤ Vậy n ∈ {1; 3; -11; 15}
c)(n + 7) ⋮ (n - 3)
Do đó ta có (n + 7) = (n - 3) + 10
Nên 10 ⋮ n - 3
Vậy n - 3 ∈ Ư(10) = {-1; 1; -2; 2; -5; 5; -10; 10}
Ta có bảng sau :
| n - 3 | -1 | 1 | -2 | 2 | -5 | 5 | -10 | 10 |
| n | 2 | 4 | 1 | 5 | -2 | 8 | -7 | 13 |
➤ Vậy n ∈ {2; 4; 1; 5; -2; 8; -7; 13}
d)(2n + 16) ⋮ (n + 1)
(2n + 16) ⋮ 2(n + 1)
Do đó ta có (2n + 16) = 2(n + 1) + 14
Nên 14 ⋮ n + 1
Vậy n + 1 ∈ Ư(14) = {-1; 1; -2; 2; -7; 7; -14; 14}
Ta có bảng sau :
| n + 1 | -1 | 1 | -2 | 2 | -7 | 7 | -14 | 14 |
| n | -2 | 0 | -3 | 1 | -8 | 6 | -15 | 13 |
➤ Vậy n ∈ {-2; 0; -3; 1; -8; 6; -15; 13}
e)(2n + 3) ⋮ n
2n + 3 ⋮ 2(n + 0)
Do đó ta có 2n + 3 = n + 3
Nên 3 ⋮ n
Vậy n ∈ Ư(3) = {-1; 1; -3; 3}
➤ Vậy n ∈ {-1; 1; -3; 3}
f)(5n + 12) ⋮ (n - 3)
(5n + 12) ⋮ 5(n - 3)
Do đó ta có (5n + 12) = 5(n - 3) + 27
Nên 27 ⋮ n - 3
Vậy n - 3 ∈ Ư(27) = {-1; 1; -3; 3; -9; 9; -27; 27}
Ta có bảng sau :
| n - 3 | -1 | 1 | -3 | 3 | -9 | 9 | -27 | 27 |
| n | 2 | 4 | 0 | 6 | -6 | 12 | -24 | 30 |
➤ Vậy n ∈ {2; 4; 0; 6; -6; 12; -24; 30}
7 tháng 3 2019
a) ta có Ư (7) = (-1;+1;-7;+7)
xét các trường hợp :
1: 2n + 1 = -1 => n= (-1) -1 :2=-1
2: 2n + 1 = 1 => n= 1 -1 : 2 = 0
3: 2n + 1 = -7 => n= -7 -1 : 2 = -3
4: 2n + 1 = 7 => n= 7 -1 : 2 = 3
mỏi quá trường hợp còn lại q1 tự sét nha
7 tháng 3 2019
Câu a, trên làm rồi và câu b làm tương tự mk làm các câu sau nha
c) ta có n-6 chia hết cho n-6
=>n-6-(n+5) chia hết cho n-6
=>-11 chia hết cho n-6
Làm tương tự