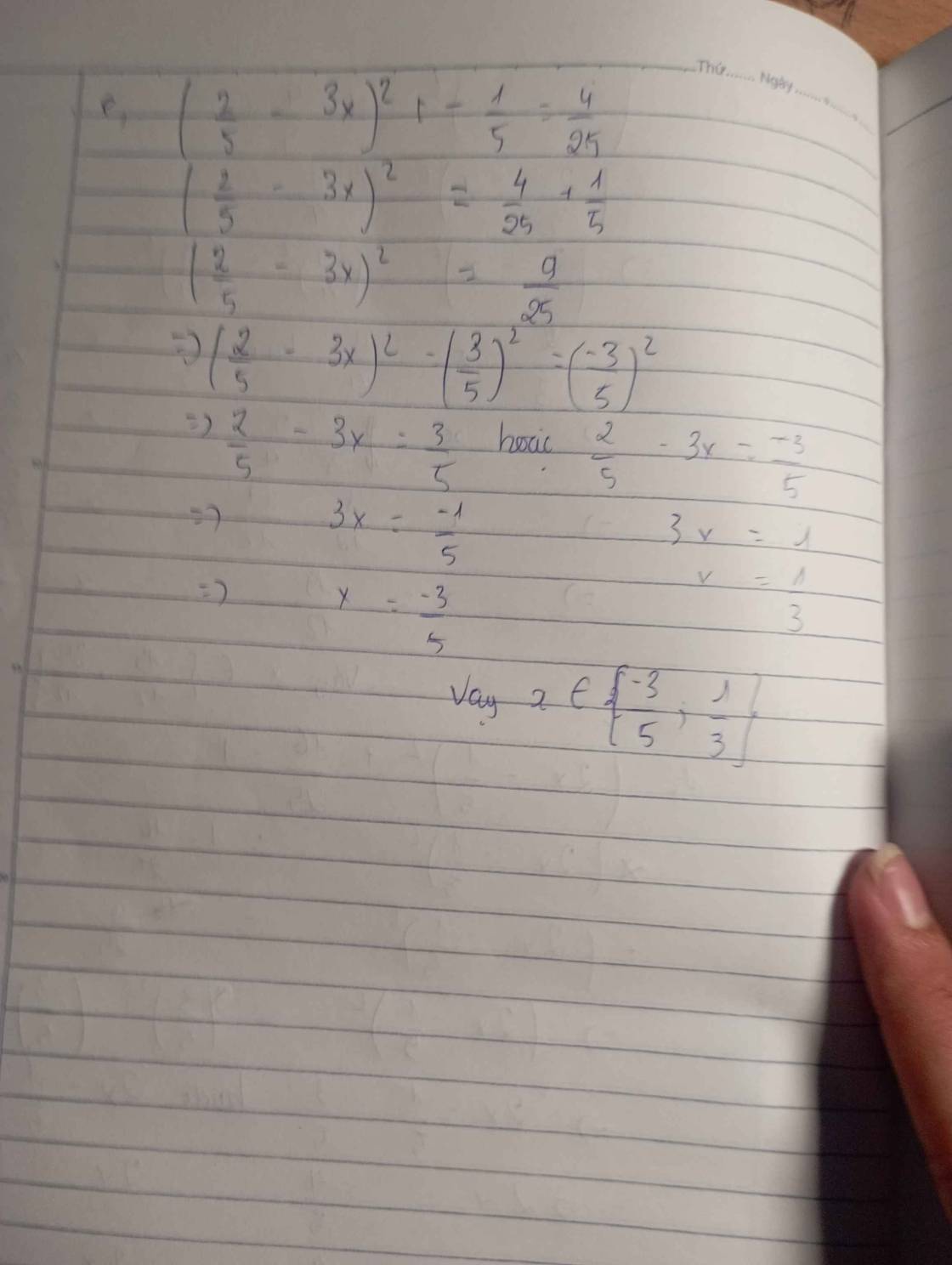K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
11 tháng 12 2022
\(=25\cdot\dfrac{-1}{27}+\dfrac{1}{5}-2\cdot\dfrac{1}{4}-\dfrac{1}{2}\)
=-25/27+1/5-1
=-52/27+1/5
=-260/135+27/135
=-233/135
22 tháng 6 2016
\(a,\left(\frac{3}{8}+-\frac{3}{4}+\frac{7}{12}\right):\frac{5}{6}+\frac{1}{2}\)
= \(\left(-\frac{3}{8}+\frac{7}{12}\right):\frac{5}{6}+\frac{1}{2}\)
= \(\frac{5}{24}:\frac{5}{6}+\frac{1}{2}\)
= \(\frac{1}{4}+\frac{1}{2}\)
= \(\frac{3}{4}\)
b)\(-\frac{7}{3}.\frac{5}{9}+\frac{4}{9}.\left(-\frac{3}{7}\right)+\frac{17}{7}\)
=\(-\frac{35}{27}+\left(-\frac{4}{21}\right)+\frac{17}{7}\)
= \(-\frac{35}{27}+\frac{47}{21}\)
= \(\frac{178}{189}\)
c) \(\frac{117}{13}-\left(\frac{2}{5}+\frac{57}{13}\right)\)
= \(\frac{117}{13}-\frac{311}{65}\)
= \(\frac{274}{65}\)
d) \(\frac{2}{3}-0,25:\frac{3}{4}+\frac{5}{8}.4\)
= \(\frac{2}{3}-\frac{1}{4}:\frac{3}{4}+\frac{5}{8}.4\)
= \(\frac{2}{3}-\frac{1}{3}+\frac{5}{2}\)
= \(\frac{1}{3}+\frac{5}{2}\)
= \(\frac{17}{6}\)
TN
6 tháng 8 2016
1)
a. \(\left(3x^2-50\right)^2=5^4\)
\(\Leftrightarrow3x^4-50=625\)
\(\Leftrightarrow3x^4=675\)
\(\Leftrightarrow x^4=225\)
\(\Leftrightarrow x=\sqrt{15}\)
2)
a. \(\frac{\left(3^4-3^3\right)^4}{27^3}=\frac{3^{16}-3^{12}}{\left(3^3\right)^3}=\frac{3^{12}.3^4-3^{12}}{3^9}=\frac{3^{12}\left(3^4-1\right)}{3^9}\)
\(=\frac{3^{12}.80}{3^9}=3^3.80=27.80=2160\)
b. \(\frac{25^3}{\left(5^5-5^3\right)^2}=\frac{\left(5^2\right)^3}{5^{10}-5^6}=\frac{5^6}{5^6.5^4-5^6}=\frac{5^6}{5^6\left(5^4-1\right)}\)
\(=\frac{5^6}{5^6.624}=\frac{1}{624}\)
5 tháng 8 2017
1. So sánh
a) \(25^{50}\) và \(2^{300}\)
\(25^{50}=25^{1.50}=\left(25^1\right)^{50}=25^{50}\)
\(2^{300}=2^{6.50}=\left(2^6\right)^{50}=64^{50}\)
Vì \(25< 64\) nên \(25^{50}< 64^{50}\)
Vậy \(25^{50}< 2^{300}\)
b) \(625^{15}\) và \(12^{45}\)
\(625^{15}=625^{1.15}=\left(625^1\right)^{15}=625^{15}\)
\(12^{45}=12^{3.15}=\left(12^3\right)^{15}=1728^{15}\)
Vì \(625< 1728\) nên \(625^{15}< 1728^{15}\)
Vậy \(625^{15}< 12^{45}\)
QD
5 tháng 8 2017
1.So sánh
a)\(25^{50}\) và \(2^{300}\)
Ta có : \(2^{300}=\left(2^6\right)^{50}=64^{50}\)
Vì \(25^{50}< 64^{50}\) nên \(25^{50}< 2^{300}\)
b)\(625^{15}\) và \(12^{45}\)
Ta có : \(12^{45}=\left(12^3\right)^{15}=1728^{15}\)
Vì \(625^{15}< 1728^{15}\) nên \(625^{15}< 12^{45}\)
5 tháng 10 2020
Bài 1 :
a) \(\frac{12}{21}-\frac{3}{7}+\left(-\frac{2}{3}\right)=\frac{4}{7}-\frac{3}{7}+\left(-\frac{2}{3}\right)=\frac{1}{7}-\frac{2}{3}=-\frac{11}{21}\)
b) \(\left(-\frac{25}{13}\right)+\left(-\frac{9}{17}\right)+\frac{12}{13}+\left(-\frac{25}{17}\right)\)
\(=\left[\left(-\frac{25}{13}\right)+\frac{12}{13}\right]+\left[\left(-\frac{9}{17}\right)+\left(-\frac{25}{17}\right)\right]\)
\(=-1+\left(-2\right)=-1-2=-3\)
c) \(\frac{5}{9}\cdot\frac{7}{13}+\frac{5}{9}\cdot\frac{9}{13}-\frac{5}{9}\cdot\frac{3}{13}=\frac{5}{9}\left(\frac{7}{13}+\frac{9}{13}-\frac{3}{13}\right)=\frac{5}{9}\cdot1=\frac{5}{9}\)
Bài 2 :
a) \(\frac{2}{3}x+\frac{5}{7}=\frac{3}{10}\)
=> \(\frac{2}{3}x=\frac{3}{10}-\frac{5}{7}=-\frac{29}{70}\)
=> \(x=\left(-\frac{29}{70}\right):\frac{2}{3}=\left(-\frac{29}{70}\right)\cdot\frac{3}{2}=-\frac{87}{140}\)
b) \(x:\frac{5}{2}-\frac{1}{2}=-\frac{2}{3}\)
=> \(x:\frac{5}{2}=-\frac{2}{3}+\frac{1}{2}=-\frac{1}{6}\)
=> \(x=\left(-\frac{1}{16}\right)\cdot\frac{5}{2}=-\frac{5}{32}\)
c) Bạn chỉ cần xét hai trường hợp âm và dương thôi :>