Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) =
=
b) =
=
=
. ( Với điều kiện b # 1)
c) \(\dfrac{a^{\dfrac{1}{3}}b^{-\dfrac{1}{3}-}a^{-\dfrac{1}{3}}b^{\dfrac{1}{3}}}{\sqrt[3]{a^2}-\sqrt[3]{b^2}}\)= =
=
( với điều kiện a#b).
d) \(\dfrac{a^{\dfrac{1}{3}}\sqrt{b}+b^{\dfrac{1}{3}}\sqrt{a}}{\sqrt[6]{a}+\sqrt[6]{b}}\) = =
=
=

Câu a, b thì Nguyễn Quang Duy làm đúng rồi.
c) \(a^{\dfrac{4}{3}}:\sqrt[3]{a}=a^{\dfrac{4}{3}}:a^{\dfrac{1}{3}}=a^{\dfrac{4}{3}-\dfrac{1}{3}}=a\)
d) \(\sqrt[3]{b}:b^{\dfrac{1}{6}}=b^{\dfrac{1}{3}}:b^{\dfrac{1}{6}}=b^{\dfrac{1}{3}-\dfrac{1}{6}}=b^{\dfrac{1}{6}}\)

a)
Đặt \(\frac{x}{2}=t\Rightarrow 3^{2t}-4=5^t\)
\(\Leftrightarrow 9^t-5^t=4\)
TH1: \(t>1\Rightarrow 9^t-5^t< 4^t\)
\(\Leftrightarrow 9^t< 4^t+5^t\)
\(\Leftrightarrow 1< \left(\frac{4}{9}\right)^t+\left(\frac{5}{9}\right)^t\) \((*)\)
Ta thấy vì \(\frac{4}{9};\frac{5}{9}<1 \), do đó với \(t>1\Rightarrow \left\{\begin{matrix} \left(\frac{4}{9}\right)^t< \frac{4}{9}\\ \left(\frac{5}{9}\right)^t< \frac{5}{9}\end{matrix}\right.\)
\(\Rightarrow \left(\frac{4}{9}\right)^t+\left(\frac{5}{9}\right)^t< \frac{4}{9}+\frac{5}{9}=1\) (mâu thuẫn với (*))
TH2: \(t<1 \) tương tự TH1 ta cũng suy ra mâu thuẫn
do đó \(t=1\Rightarrow x=2\)
b)
Ta có: \(5^{2x}=3^{2x}+2.5^x+2.3^x\)
\(\Leftrightarrow (5^{2x}-2.5^{x}+1)=3^{2x}+2.3^x+1\)
\(\Leftrightarrow (5^x-1)^2=(3^x+1)^2\)
\(\Leftrightarrow (5^x-3^x-2)(5^x+3^x)=0\)
Dễ thấy \(5^x+3^x>0\forall x\in\mathbb{R}\Rightarrow 5^x-3^x-2=0\)
\(\Leftrightarrow 5^x-3^x=2\)
\(\Leftrightarrow 5^x=3^x+2\)
Đến đây ta đưa về dạng giống hệt phần a, ta thu được nghiệm \(x=1\)
c)
\((2-\sqrt{3})^x+(2+\sqrt{3})^x=4^x\)
\(\Leftrightarrow \left(\frac{2-\sqrt{3}}{4}\right)^x+\left(\frac{2+\sqrt{3}}{4}\right)^x=1\)
TH1: \(x>1\)
Vì \(\frac{2+\sqrt{3}}{4};\frac{2-\sqrt{3}}{4}<1;x> 1 \Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x< \frac{2-\sqrt{3}}{4};\left ( \frac{2+\sqrt{3}}{4} \right )^x< \frac{2+\sqrt{3}}{4}\)
\(\Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x+\left ( \frac{2+\sqrt{3}}{4} \right )^x<\frac{2-\sqrt{3}}{4}+\frac{2+\sqrt{3}}{4}=1\) (vô lý)
TH2: \(x<1 \)
\(\frac{2+\sqrt{3}}{4};\frac{2-\sqrt{3}}{4}<1; x< 1 \Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x> \frac{2-\sqrt{3}}{4};\left ( \frac{2+\sqrt{3}}{4} \right )^x> \frac{2+\sqrt{3}}{4}\)
\(\Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x+\left ( \frac{2+\sqrt{3}}{4} \right )^x>\frac{2-\sqrt{3}}{4}+\frac{2+\sqrt{3}}{4}=1\) (vô lý)
Do đó \(x=1\)

a) Xét hàm số y = f(x)=12x4−3x2+32f(x)=12x4−3x2+32 (C) có tập xác định: D = R
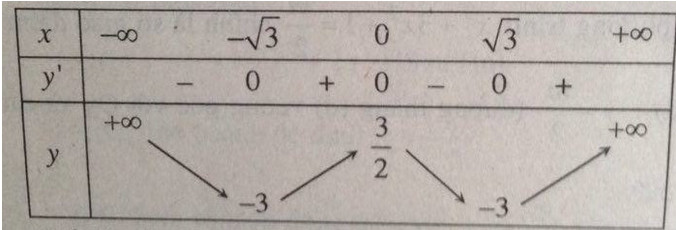
y’ = 2x3 – 6x = 2x(x2 – 3)
y’ = 0 ⇔ x = 0, x = ±√3
Bảng biến thiên:
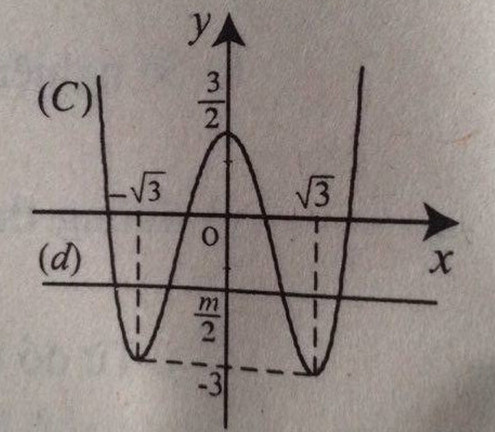
Đồ thị hàm số:
b)
y’’ = 6x2 – 6x
y’’ = 0 ⇔ 6x2 – 6x = 0 ⇔ x = ± 1
y’(-1) = 4, y’’(1) = -4, y(± 1) = -1
Tiếp tuyến của (C) tại điểm (-1, -1) là : y = 4(x+1) – 1= 4x+3
Tiếp tuyến của (C) tại điểm (1, -1) là: y = -4(x-1) – 1 = -4x + 3
c) Ta có: \(x^4-6x^2+3=m\)\(\Leftrightarrow\dfrac{x^4}{2}-3x^2+\dfrac{3}{2}=\dfrac{m}{2}\).
Số nghiệm của (1) là số giao điểm của (C) và đường thẳng (d) : \(y=\dfrac{m}{2}\).
Dễ thấy:
m < -6: ( 1) vô nghiệm
m = -6 : (1) có 2 nghiệm
-6 < m < 3: (1) có 4 nghiệm
m = 3: ( 1) có 3 nghiệm
m > 3: (1) có 2 nghiệm

a) Tập xác định : D = R { 1 }.
> 0, ∀x
1.
Hàm số đồng biến trên các khoảng : (-∞ ; 1), (1 ; +∞).
b) Tập xác định : D = R { 1 }.
< 0, ∀x
1.
Hàm số nghịch biến trên các khoảng : (-∞ ; 1), (1 ; +∞).
c) Tập xác định : D = (-∞ ; -4] ∪ [5 ; +∞).
∀x ∈ (-∞ ; -4] ∪ [5 ; +∞).
Với x ∈ (-∞ ; -4) thì y’ < 0; với x ∈ (5 ; +∞) thì y’ > 0. Vậy hàm số nghịch biến trên khoảng (-∞ ; -4) và đồng biến trên khoảng (5 ; +∞).
d) Tập xác định : D = R { -3 ; 3 }.
< 0, ∀x
±3.
Hàm số nghịch biến trên các khoảng : (-∞ ; -3), (-3 ; 3), (3 ; +∞).

Bài 1:
Đặt \(\left(\frac{3}{2}\right)^x=a\) \((a>0)\)
PT tương đương với:
\(\left(\frac{9}{4}\right)^x-2.\left(\frac{3}{2}\right)^x+m^2=0\)
\(\Leftrightarrow a^2-2a+m^2=0\) (1)
-Trước tiên, để pt đầu tiên có hai nghiệm phân biệt thì (1) cũng phải có hai nghiệm phân biệt \(\rightarrow \) \(\Delta'=1-m^2>0\Leftrightarrow -1< m< 1\)
Áp dụng hệ thức Viete với \(a_1,a_2\) là nghiệm của (1) \(\left\{\begin{matrix} a_1+a_2=2\\ a_1a_2=m^2\end{matrix}\right.\)
-Vì \(a\) luôn dương nên \(\left\{\begin{matrix} a_1+a_2>0\\ a_1a_2>0\end{matrix}\right.\Leftrightarrow m^2>0 \Leftrightarrow m\neq 0\)
-Xét đk cuối cùng, để pt đầu tiên có hai nghiệm trái dấu, tức \(x<0\) hoặc $x>0$ thì \(a<1\) hoặc \(a>1\), hay \((a_1-1)(a_2-1)< 0\)
\(\Leftrightarrow a_1a_2-(a_1+a_2)+1< 0\Leftrightarrow m^2<1\Leftrightarrow -1< m< 1\)
Vậy \(-1< m< 1; m\neq 0\)
Bài 2:
Đặt \(2^x=a\Rightarrow \) \(4^x-2m.2^x+2m=0\) tương đương với:
\(a^2-2ma+2m=0\) (1)
Để pt đầu tiên có hai nghiệm phân biệt thì (1) cũng phải có hai nghiệm phân biệt
\(\Rightarrow \Delta'=m^2-2m>0\Leftrightarrow m< 0\) hoặc $m>2$
Áp dugnj hệ thức viete với $a_1,a_2$ là hai nghiệm của phương trình:
\(a_1a_2=2m\Leftrightarrow 2^{x_1}.2^{x_2}=2m\Leftrightarrow 2^{x_1+x_2}=2m\Leftrightarrow 8=2m\rightarrow m=4\)
(thỏa mãn)
Vậy \(m=4\)
ĐKXĐ: \(-2\le x\le2\)
Với \(-2\le x\le\frac{2}{3}\Rightarrow6x-4\le0\Rightarrow VT\ge VP\) BPT luôn đúng
- Với \(\frac{2}{3}\le x\le3\) ta có:
\(VT^2=\left(\sqrt{2x+4}+2\sqrt{2-x}\right)^2=12-2x+4\sqrt{2\left(4-x^2\right)}\ge8\)
\(\Rightarrow VT\ge2\sqrt{2}\)
\(VP=\frac{6x-4}{5\sqrt{x^2+1}}< \frac{6x-4}{5}\le\frac{12-4}{5}=\frac{8}{5}< 2\sqrt{2}\)
\(\Rightarrow VT>VP\)
Vậy BPT luôn đúng với mọi \(x\in\left[-2;2\right]\Rightarrow\left\{{}\begin{matrix}a=-2\\b=2\end{matrix}\right.\) \(\Rightarrow P=-10\)
Cm VT2 ≥ 8 như nào vậy bạn, mình không hiểu lắm