Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D
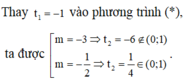
Tất nhiên đến đây mà vội vàng kết luận thì chưa hoàn thành, các em có thể dễ thấy trường hợp còn lại không có m thỏa mãn yêu cầu bài toán
Trường hợp phương trình(*) có một nghiệm t 1 = 1 (có hai nghiệm x) và một nghiệm - 1 < t 2 ≤ 0 (có ba nghiệm x).
Rất dễ để tìm được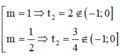 
nhưng rõ ràng không có m theo yêu cầu.
Vậy ta kết luận
m
=
-
1
2
thỏa mãn yêu cầu bài toán và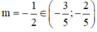 
.
§ Bổ trợ kiến thức: Không dễ để các em có thể nhận ra cả 2 trường hợp này trong cùng một bài toán, cho nên khi gặp một số trường hợp đã giải ra kết quả mà có khả năng là đáp án đúng cao thì các em nên mạnh dạn bỏ hẳn trường hợp còn lại để tránh việc mất nhiều thời gian vào các trường hợp không đâu, ở đây phương án bên dưới cho rất nhẹ nên các em có thể dễ dàng kết luận luôn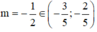 
và chọn đáp án đúng.
\(\Leftrightarrow1-2sin^2x+\left(2m-3\right)sinx+m-2=0\)
\(\Leftrightarrow2sin^2x-\left(2m-3\right)sinx-m+1=0\)
\(\Leftrightarrow2sin^2x+sinx-2\left(m-1\right)sinx-\left(m-1\right)=0\)
\(\Leftrightarrow sinx\left(2sinx+1\right)-\left(m-1\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2sinx+1\right)\left(sinx-m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=-\dfrac{1}{2}\\sinx=m-1\end{matrix}\right.\)
Pt có đúng 2 nghiệm thuộc khoảng đã cho khi và chỉ khi:
\(\left\{{}\begin{matrix}m-1\ne-\dfrac{1}{2}\\-1\le m-1\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\0\le m\le2\end{matrix}\right.\)
\(sin^2x-2m.sinx.cosx-sinx.cosx+2mcos^2x=0\)
\(\Leftrightarrow sinx\left(sinx-cosx\right)-2mcosx\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx-2m.cosx\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=cosx\\sinx=2m.cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}tanx=1\\tanx=2m\end{matrix}\right.\)
Do \(tanx=1\) ko có nghiệm đã cho nên \(tanx=2m\) phải có nghiệm trên khoảng đã cho
\(\Rightarrow tan\left(\dfrac{\pi}{4}\right)< 2m< tan\left(\dfrac{\pi}{3}\right)\)
\(\Rightarrow1< 2m< \sqrt[]{3}\)
\(\Rightarrow m\in\left(\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\) (hoặc có thể 1 đáp án là tập con của tập này cũng được)
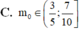
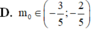
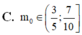
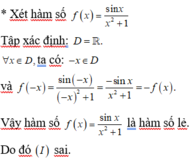
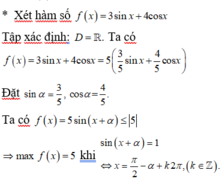
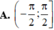
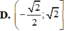
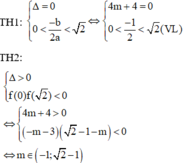
Đáp án D
Tất nhiên đến đây mà vội vàng kết luận thì chưa hoàn thành, các em có thể dễ thấy trường hợp còn lại không có m thỏa mãn yêu cầu bài toán.
Trường hợp phương trình (*) có một nghiệm t 1 = 1 (có hai nghiệm x) và một nghiệm - 1 < t 2 ≤ 0 (có ba nghiệm x).
Rất dễ để tìm được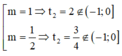
nhưng rõ ràng không có m theo yêu cầu.
Vậy ta kết luận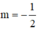
thỏa mãn yêu cầu bài toán và 
.
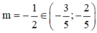§ Bổ trợ kiến thức: Không dễ để các em có thể nhận ra cả 2 trường hợp này trong cùng một bài toán, cho nên khi gặp một số trường hợp đã giải ra kết quả mà có khả năng là đáp án đúng cao thì các em nên mạnh dạn bỏ hẳn trường hợp còn lại để tránh việc mất nhiều thời gian vào các trường hợp không đâu, ở đây phương án bên dưới cho rất nhẹ nên các em có thể dễ dàng kết luận luôn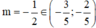
và chọn đáp án đúng.