Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Điều kiện: \(\left\{{}\begin{matrix}4x+2>0\\x-1>0\\x>0\end{matrix}\right.\)
Hay là: \(x>1\)
Khi đó biến đổi pương trình như sau:
\(\ln\dfrac{4x+2}{x-1}=\ln x\)
\(\Leftrightarrow\dfrac{4x+2}{x-1}=x\)
\(\Leftrightarrow4x+2=x\left(x-1\right)\)
\(\Leftrightarrow x^2-5x-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{5+\sqrt{33}}{2}\\x_2=\dfrac{5-\sqrt{33}}{2}\left(loại\right)\end{matrix}\right.\)
Vậy nghiệm của phương trình là: \(x=\dfrac{5+\sqrt{33}}{2}\)
b) Điều kiện: \(\left\{{}\begin{matrix}3x+1>0\\x>0\end{matrix}\right.\)
Hay là: \(x>0\)
Biến đổi phương trình như sau:
\(\log_2\left(3x+1\right)\log_3x-2\log_2\left(3x+1\right)=0\)
\(\Leftrightarrow\log_2\left(3x+1\right)\left(\log_3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\log_2\left(3x+1\right)=0\\\log_3x=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+1=2^0\\x=3^2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=9\end{matrix}\right.\)
Vậy nghiệm là x = 9.

a) Đặt t = 13x > 0 ta được phương trình:
13t2 – t – 12 = 0 ⇔ (t – 1)(13t + 12) = 0
⇔ t = 1 ⇔ 13x = 1 ⇔ x = 0
b)
Chia cả hai vế phương trình cho 9x ta được phương trình tương đương
(1+(23)x)(1+3.(23)x)=8.(23)x(1+(23)x)(1+3.(23)x)=8.(23)x
Đặt t=(23)xt=(23)x (t > 0) , ta được phương trình:
(1 + t)(1 + 3t) = 8t ⇔ 3t2 – 4t + 1 = 0 ⇔ t∈{13,1}t∈{13,1}
Với t=13t=13 ta được nghiệm x=log2313x=log2313
Với t = 1 ta được nghiệm x = 0
c) Điều kiện: x > 2
Vì nên phương trình đã cho tương đương với:
[log3(x−2)=0log5x=1⇔[x=3x=5[log3(x−2)=0log5x=1⇔[x=3x=5
d) Điều kiện: x > 0
log22x – 5log2x + 6 = 0
⇔(log2x – 2)(log2x – 3) = 0
⇔ x ∈ {4, 8}

d) Điều kiện \(\begin{cases}x\ne0\\\log_2\left|x\right|\ge0\end{cases}\)\(\Leftrightarrow\left|x\right|\ge\)1
Phương trình đã cho tương đương với :
\(\log_2\left|x\right|^{\frac{1}{2}}-4\sqrt{\log_{2^2}\left|x\right|}-5=0\)
\(\Leftrightarrow\frac{1}{2}\log_2\left|x\right|-4\sqrt{\frac{1}{4}\log_2\left|x\right|}-5=0\)
Đặt \(t=\sqrt{\frac{1}{2}\log_2\left|x\right|}\) \(\left(t\ge0\right)\) thì phương trình trở thành :
\(t^2-4t-5=0\) hay t=-1 V t=5
Do \(t\ge0\) nên t=5
\(\Rightarrow\frac{1}{2}\log_2\left|x\right|=25\Leftrightarrow\log_2\left|x\right|=50\Leftrightarrow\left|x\right|=2^{50}\) Thỏa mãn
Vậy \(x=\pm2^{50}\) là nghiệm của phương trình
c) Điều kiện x>0. Phương trình đã cho tương đương với :
\(x^{lg^2x^2-3lgx-\frac{9}{2}}=\left(10^{lgx}\right)^{-2}\)
\(\Leftrightarrow lg^2x^2-3lgx-\frac{9}{2}=-2\)
\(\Leftrightarrow8lg^2x-6lgx-5=0\)
Đặt \(t=lgx\left(t\in R\right)\) thì phương trình trở thành
\(8t^2-6t-5=0\) hay\(t=-\frac{1}{2}\) V \(t=\frac{5}{4}\)
Với \(t=-\frac{1}{2}\) thì \(lgx=-\frac{1}{2}\Leftrightarrow x=\frac{1}{\sqrt{10}}\)
Với \(t=\frac{5}{4}\) thì \(lgx=\frac{5}{4}\Leftrightarrow x=\sqrt[4]{10^5}\)
Vậy phương trình đã cho có nghiệm \(x=\sqrt[4]{10^5}\) và \(x=\frac{1}{\sqrt{10}}\)

Bạn ko phân biệt được "hoặc" và "và" trong toán học rồi
"Hoặc" là có thể cái này xảy ra, cái kia xảy ra đều được, nhưng "và" thì phải 2 thứ đồng thời xảy ra. Mà trên đời làm gì tồn tại số thực nào vừa lớn hơn 3 vừa nhỏ hơn 2 đâu bạn
Bạn có thể dễ dàng kiểm chứng kết quả bài toán bằng MODE-7 của casio mà :D
\(log_2x-log_2x.log_3x+log_3x-1>0\)
\(\Leftrightarrow log_2x\left(1-log_3x\right)-\left(1-log_3x\right)>0\)
\(\Leftrightarrow\left(log_2x-1\right)\left(1-log_3x\right)>0\)
\(\Rightarrow2< x< 3\)

d) Điều kiện x>0. Áp dụng công thức đổi cơ số, ta có :
\(\log_2x+\log_3x+\log_4x=\log_{20}x\)
\(\Leftrightarrow\log_2x+\frac{\log_2x}{\log_23}+\frac{\log_2x}{\log_24}=\frac{\log_2x}{\log_220}\)
\(\Leftrightarrow\log_2x\left(1+\frac{1}{\log_23}+\frac{1}{2}+\frac{1}{\log_220}\right)=0\)
\(\Leftrightarrow\log_2x\left(\frac{3}{2}+\log_22-\log_{20}2\right)=0\)
Ta có \(\frac{3}{2}+\log_22-\log_{20}2>\frac{3}{2}+0-1>0\)
Do đó, từ phương trình trên, ta phải có \(\log_2x=0\) hay \(x=2^0=1\)
Vậy nghiệm duy nhất của phương trình là \(x=1\)
c) Điều kiện x>0, đưa về cùng cơ số 5, ta có :
\(\log_5x^3+3\log_{25}x+\log_{\sqrt{25}}\sqrt{x^3}=\frac{11}{2}\)
\(\Leftrightarrow3\log_5x+3\log_{5^2}x+\log_{5^{\frac{3}{2}}}x^{\frac{3}{2}}=\frac{11}{2}\)
\(\Leftrightarrow3\log_5x+3\frac{1}{2}\log_5x+\frac{3}{2}.\frac{2}{3}\log_5x=\frac{11}{2}\)
\(\Leftrightarrow\frac{11}{2}\log_5x=\frac{11}{2}\)
\(\Leftrightarrow\log_5x=1\)
\(\Leftrightarrow x=5^1=5\) thỏa mãn
Vậy phương trình chỉ có 1 nghiệ duy nhất \(x=5\)
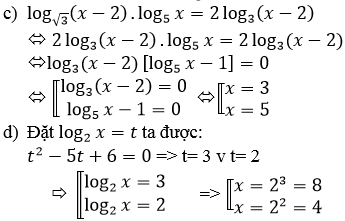
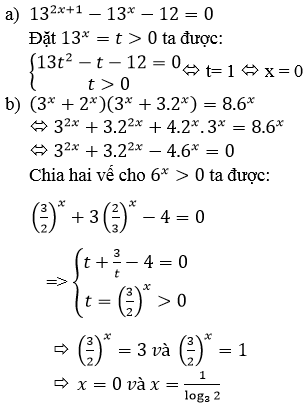

\(log_3x-log_5x.log_2x=0\)
\(\Leftrightarrow\frac{log_2x}{log_23}-\frac{log_2x}{log_25}.log_2x=0\)
\(\Leftrightarrow log_2x\left(\frac{1}{log_23}-\frac{log_2x}{log_25}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}log_2x=0\\\frac{1}{log_23}=\frac{log_2x}{log_25}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}log_2x=0\\log_2x=\frac{log_25}{log_23}=log_35\end{matrix}\right.\)
\(\Rightarrow T=log_2\left(x_1x_2\right)=log_2x_1+log_2x_2=0+log_35=log_35\)