Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kéo dài DF cắt AB tại E như sau:
 |
- Vì ABCD là hình thang nên AB , AE \(\backslash\backslash\) DC.
Suy ra, \(\widehat{EBF}=\widehat{DCF}\) (hai góc so le trong)
\(\widehat{BFE}=\widehat{CFD}\) (hai góc đối đỉnh).
Xét tam giác BEF và tam giác CDF có : \(\widehat{EBF}=\widehat{DCF}\) (cmt)
BF = FC ( F là trung điểm của BC)
\(\widehat{BFE}=\widehat{CFD}\) (cmt)
Vậy . tam giác BEF = tam giác CDF
Suy ra : FE = FD
Ta có : Diện tích hình ABDF + Diện tích hình CDF = Diện tích hình ABCD
Diện tích hình ABDF + Diện tích hình BEF = Diện tích hình ADE
Mà : tam giác BEF = tam giác CDF
Suy ra : diện tích ABCD bằng diện tích tam giác ADE
Với FE = FD, ta có hai tam giác ADF và AEF có đáy bằng nhau, cùng chung đường cao hạ từ A.
Suy ra, diện tích tam giác AFE bằng diện tích tam giác ADF.
Mà : diện tích tam giác AFE + diện tích tam giác ADF = diện tích tam giác ADE
Nên diện tích tam giác ADE bằng hai lần diện tích tam giác AFD và bằng : 2 x 10 = 20 cm2.

Do ABCD là hình thoi nên hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường
Diện tích tam giác ABC là
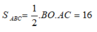
Suy ra: BO.AC = 32
Diện tích hình thoi ABCD là:
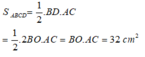
Chọn đáp án B

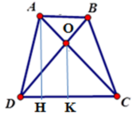
Kẻ AH ⊥ DC; OK ⊥ DC tại H, K suy ra AH // OK
Chiều cao của hình thang: AH = 2 S A B C D A B + C D = 2.48 4 + 8 = 8 (cm)
Vì AB // CD (do ABCD là hình thang) nên theo định lý Ta-lét ta có
O C O A = C D A B = 8 4 = 2 ⇒ O C O A + O C = 2 2 + 1 ⇒ O C A C = 2 3
Vì AH // OK (cmt) nên theo định lý Ta-lét cho tam giác AHC ta có:
O K A H = O C A C = 2 3 => OK = 2 3 AH => OK = 2 3 .6 = 4(cm)
Do đó S C O D = 1 2 OK.DC = 1 2 . 16 3 .8 = 64 3 c m 2
Đáp án: A

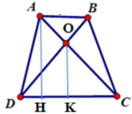
Kẻ AH ⊥ DC; OK ⊥ DC tại H, K suy ra AH // OK
Chiều cao của hình thang: AH = 2 S A B C D A B + C D = 2.36 4 + 8 = 6 (cm)
Vì AB // CD (do ABCD là hình thang) nên theo định lý Ta-lét ta có
O C O A = C D A B = 8 4 = 2 ⇒ O C O A + O C = 2 2 + 1 ⇒ O C A C = 2 3
Vì AH // OK (cmt) nên theo định lý Ta-lét cho tam giác AHC ta có:
O K A H = O C A C = 2 3 => OK = 2 3 AH => OK = 2 3 .6 = 4(cm)
Do đó S C O D = 1 2 OK.DC = 1 2 .4.8 = 16cm2
Đáp án: C


trả lời giúp mik sơm mik cảm ơn
Tham khảo: https://lazi.vn/edu/exercise/cho-hinh-thang-abcd-nhu-hinh-ve-biet-dien-tich-tam-giac-afd-10cm2-va-f-la-trung-diem-cua-bc-hoi-dien-tich