NP
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QB
0
CM
20 tháng 10 2019
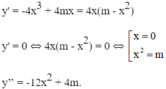
- Nếu m ≤ 0, phương trình y’ = 0 có nghiệm duy nhất x = 0.
Mà y’’(0) = 4m < 0
⇒ x = 0 là điểm cực đại và là cực trị duy nhất của hàm số.
- Nếu m > 0 thì phương trình (1) có 2 nghiệm phân biệt khác 0 nên phương trình y’= 0 có 3 nghiệm
⇒ hàm số có 3 cực trị.
PT
1
CM
9 tháng 7 2018
Ta có: x 4 - 6 x 2 + 3 = m
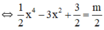
Số nghiệm của phương trình (*) chính bằng số giao điểm của đồ thị (C) và đường thẳng (d) y = m/2.
Từ đồ thị (C) nhận thấy :
+ m/2 < - 3 ⇔ m < -6
⇒ đường thẳng (d) không cắt đồ thị (C)
⇒ Phương trình vô nghiệm.
+ m/2 = -3 ⇔ m = -6
⇒ đường thẳng (d) cắt đồ thị (C) tại hai điểm cực tiểu
⇒ Phương trình có 2 nghiệm.
+ -3 < m/2 < 3/2 ⇔ -6 < m < 3
⇒ đường thẳng (d) cắt (C) tại 4 điểm phân biệt
⇒ Phương trình có 4 nghiệm.
+ m/2 = 3/2 ⇔ m = 3
⇒ đường thẳng (d) cắt (C) tại ba điểm
⇒ phương trình có 3 nghiệm.
+ m/2 > 3/2 ⇔ m > 3
⇒ đường thẳng (d) cắt (C) tại hai điểm
⇒ phương trình có hai nghiệm phân biệt.
Vậy:
+) m < - 6 thì phương trình vô nghiệm.
+) m = - 6 hoặc m > 3 thì PT có 2 nghiệm.
+) m = 3 thì PT có 3 nghiệm.
+) – 6 < m < 3 thì PT có 4 nghiệm.
LD
1
HN
17 tháng 10 2021
x4 - 2x2 - m + 3 = 0 \(\Rightarrow\) x4 - 2x2 + 3 = m.
Gọi f(x) = x4 - 2x2 + 3, D=R.
f'(x) = 4x3 - 4x = 0 \(\Rightarrow\) Hoặc x=0 hoặc x=1 hoặc x=-1.
Bảng biến thiên
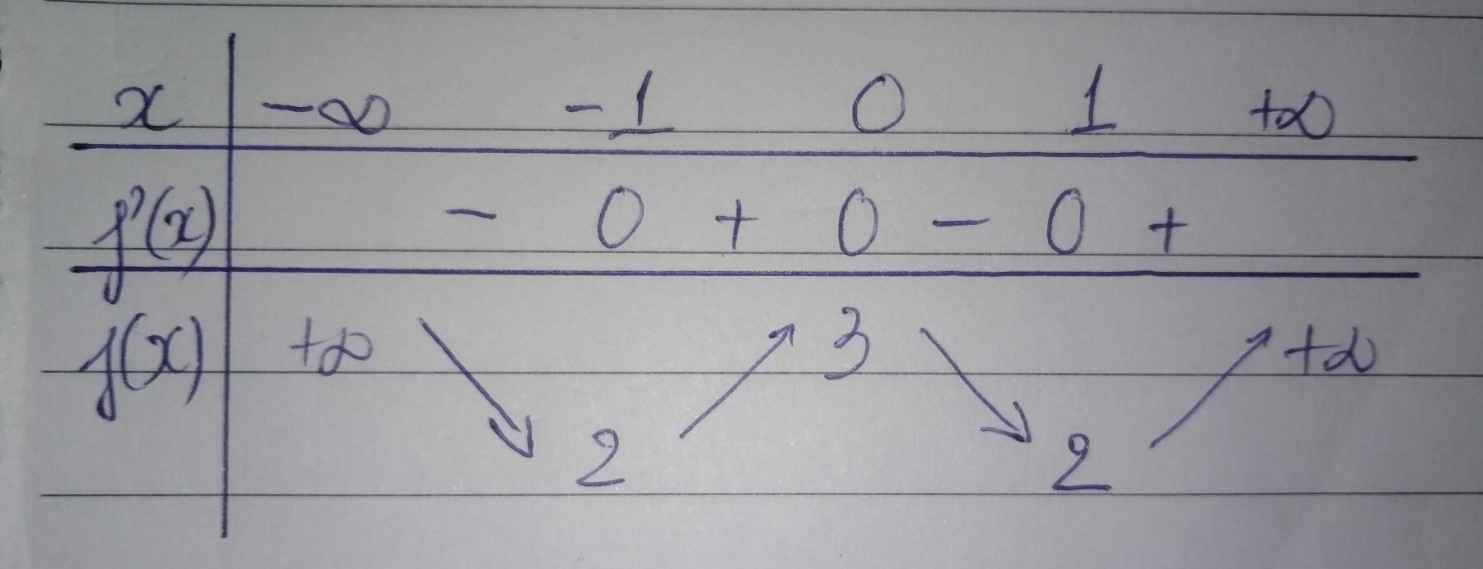
Với m<2, phương trình đã cho vô nghiệm.
Với m=2 hoặc m>3, phương trình đã cho có hai nghiệm đối nhau.
Với m=3, phương trình đã cho có ba nghiệm phân biệt.
Với 2<m<3, phương trình đã cho có bốn nghiệm phân biệt.
H
31 tháng 3 2017
a) Xét hàm số y = f(x)=12x4−3x2+32f(x)=12x4−3x2+32 (C) có tập xác định: D = R
y’ = 2x3 – 6x = 2x(x2 – 3)
y’ = 0 ⇔ x = 0, x = ±√3
Bảng biến thiên:
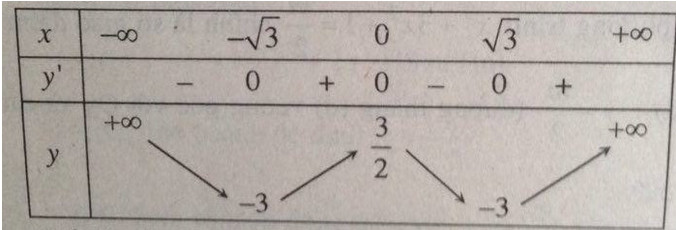
Đồ thị hàm số:
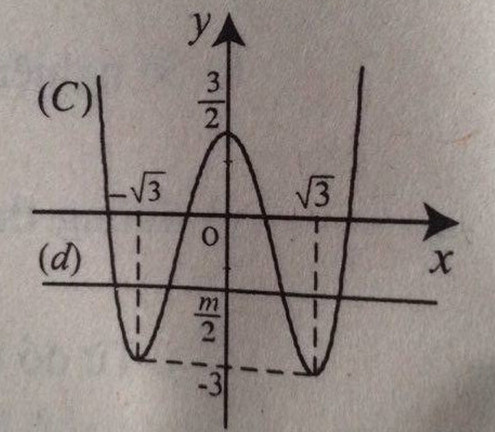
b)
y’’ = 6x2 – 6x
y’’ = 0 ⇔ 6x2 – 6x = 0 ⇔ x = ± 1
y’(-1) = 4, y’’(1) = -4, y(± 1) = -1
Tiếp tuyến của (C) tại điểm (-1, -1) là : y = 4(x+1) – 1= 4x+3
Tiếp tuyến của (C) tại điểm (1, -1) là: y = -4(x-1) – 1 = -4x + 3
c) Ta có: \(x^4-6x^2+3=m\)\(\Leftrightarrow\dfrac{x^4}{2}-3x^2+\dfrac{3}{2}=\dfrac{m}{2}\).
Số nghiệm của (1) là số giao điểm của (C) và đường thẳng (d) : \(y=\dfrac{m}{2}\).
Dễ thấy:
m < -6: ( 1) vô nghiệm
m = -6 : (1) có 2 nghiệm
-6 < m < 3: (1) có 4 nghiệm
m = 3: ( 1) có 3 nghiệm
m > 3: (1) có 2 nghiệm
CM
16 tháng 8 2017
Số giao điểm của ( C m ) và đường phân giác của góc phần tư thứ nhất là số nghiệm của phương trình:
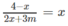
Ta có:
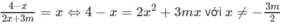
⇔ 2 x 2 + (3m + 1)x – 4 = 0 ⇔ 2 x 2 + (3m + 1) x – 4 = 0 với x ≠ −3m/2
+) Thay x = −3m/2 vào (*), ta có:
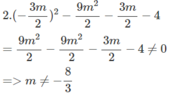
Như vậy, để x = −3m/2 không là nghiệm của phương trình (*) ta phải có m ≠ −8/3.
Ta có: ∆ = 3 m + 1 2 + 32 > 0, ∀ m. Từ đó suy ra với m ≠ −8/3 đường thẳng y = x luôn cắt ( C m ) tại hai điểm phân biệt.
H
31 tháng 3 2017
a) y= -x4 + 2mx2 – 2m + 1(Cm). Tập xác định: D = R
y ‘ = -4x3 + 4mx = -4x (x2 – m)
- Với m ≤ 0 thì y’ có một nghiệm x = 0 và đổi dấu + sang – khi qua nghiệm này. Do đó hàm số có một cực đại là x = 0
Do đó, hàm số có 2 cực trị tại x = ± √m và có một cực tiểu tại x = 0
b) Phương trình -x4 + 2mx2 – 2m + 1 = 0 luôn có nghiệm x = ± 1 với mọi m nên (Cm) luôn cắt trục hoành.
c) Theo lời giải câu a, ta thấy ngay:
với m > 0 thì đồ thị (Cm) có cực đại và cực tiểu.
31 tháng 7 2020
Câu trả lời là
0-1-2-3-4-5-6-7-8-9
a) 2057 1 số đúng, đúng vị trí
b) 4586 0 số đúng
c) 9041 1 số đúng, sai vị trí
d) 7229 2 số đúng, 1 số đúng vị trí và 1 số sai vị trí
e) 3479 1 số đúng, sai vị trí
Xét theo đk đúng sai của các số trong dãy 4 chữ số
Trước tiên, theo b), loại hết 4 số 4,5,8,6
=> Còn 0,1,2,3,7,9
Tiếp theo, theo a) và c), loại tiếp 0, vị nếu 0 đúng, không thể vừa đứng đúng và cả sai vị trí
=> Còn 1,2,3,7,9
Tiếp theo, xét trường hợp
*Nếu 7 đúng (TH1)
=> theo a), số 2 sai
=> theo TH1, a) và d), 9 đúng
Nhưng, theo e) (đk:1 số đúng), 7 và 9 không thể cùng đúng (vô lý)
Nên, 7 sai
=> Còn 1,2,3,9
*Nếu 9 đúng (TH2)
=> theo e), 3 và 7 sai
Nhưng theo TH2 và e) (đk:2 số đúng), 2 đều đúng và sai vì có tận 2 số 2 (vô lý)
Nên 9 sai
=> Còn 1,2,3 và có 2 số 2 trong dãy 4 chữ số
Xét theo vị trí đúng sai của các số trong dãy 4 chữ số
Theo a), vị trí đầu tiên thuộc về số 2 (2xxx)
Theo d), vị trí thứ hai và ba, một trong hai sẽ thuộc về số 2 khác (22xx hoặc 2x2x)
Theo c), 1 không thể đứng cuối, nên vị trí cuối thuộc về số 3 (thỏa mãn yêu cầu của e) là 3 không đứng đầu) (22x3 hoặc 2x23)
Vị trí còn lại thuộc về số 1, 2 số có khả năng là dãy số đề yêu cầu sẽ là 2213 hoặc 2123.
Xin hết!!
Dạ vâng, bài này của đstt ạ, tại vì e ko thấy lớp nào cao hơn lớp 12 nữa nên phải đánh đại là lớp 12ạ, với lại bài này dạng như tìm tổng quát chứ ko phải là tính rõ ràng ạ
Bài này không thuộc phạm vi kiến thức lớp 12.
Nếu mà thuộc thì cũng kiểu đánh đố nhau. Biện luận hạng của ma trận có tham số thì ít ra cũng phải có thông tin của những phần tử còn lại chứ bạn?