Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*x2+bx+c=0
\(\Delta=b^2-4c=b^2-4.\left(2b-4\right)=b^2-8b+16=\left(b-4\right)^2\)=>\(\sqrt{\Delta}=\left|b-4\right|\)
Với (b-4)2=0 =>b=4 =>c=4
PT có 1 nghiệm kép: \(x_1=x_2=-2\)
Với\(\Delta=\) (b-4)2>0,PT có 2 nghiệm pb: \(x_1=\frac{-b+\left|b-4\right|}{2};x_2=\frac{-b-\left|b-4\right|}{2}\)
Với b>4 thì: \(x_1=-2;x_2=\frac{-2b+4}{2}=-b+2\)
Với b<0 thì: x1=-b+2 ; x2=-2
Vậy khi c=2b-4 và b tùy ý thì PT: x2+bx+c=0 luôn có 1 nghiệm nguyên là -2

a) \(4x-7>0\Leftrightarrow4x>7\)\(\Leftrightarrow x>\frac{7}{4}\)
b) \(-5x+8>0\Leftrightarrow5x<8\Leftrightarrow x<\frac{8}{5}\)
c)\(9x-10\le0\Leftrightarrow9x\le10\)\(\Leftrightarrow x\le\frac{10}{9}\)
d) \(\left(x+1\right)^2+4\le x^2+3x+10\)\(\Leftrightarrow x^2-2x+1+4\le x^2+3x+10\)
\(\Leftrightarrow5x\ge-5\Leftrightarrow x\ge-1\)
a,
4x - 7 > 0
↔ 4x > 7
↔ x > \(\dfrac{7}{4}\)
Vậy tập nghiệm của bất phương trình là S = { x / x>\(\dfrac{7}{4}\) }
b,
-5x + 8 > 0
↔ 8 > 5x
↔ \(\dfrac{8}{5}\) > x
Vậy tập nghiệm của bất phương trình là S = { x / \(\dfrac{8}{5}\) > x }
c,
9x - 10 ≤ 0
↔ 9x ≤ 10
↔ x ≤ \(\dfrac{10}{9}\)
Vậy tập nghiệm của bất phương trình là S = { x / x ≤ \(\dfrac{10}{9}\) }
d,
( x - 1 )\(^2\) + 4 ≤ x\(^2\) + 3x + 10
↔ x\(^2\) - 2x +1 +4 ≤ x\(^2\) + 3x + 10
↔ 1 + 4 - 10 ≤ x \(^2\) - x\(^2\) + 3x + 2x
↔ -5 ≤ 5x
↔ -1 ≤ x
Vậy tập nghiệm của bất phương trình là S = { x / -1 ≤ x}

BÀI TOÁN PHỤ: CHứng minh rằng số chính phương lẻ chia cho 8 dư 1.
Giải: Xét số chính phương lẻ là \(m^2\left(m\in Z\right)\)
Như vậy m là số lẻ, đặt \(m=2n+1\)
Ta có:
\(m^2=\left(2n+1\right)^2=4n^2+4n+1=4.n.\left(n+1\right)+1\)
Vì n(n+1) là tích 2 số nguyên liên tiếp nên chia hết cho 2
\(\Rightarrow4n\left(n+1\right) \) chia hết cho 8
\(\Rightarrow4.n.\left(n+1\right)+1\) chia 8 dư 1
Vậy ta có điều phải chứng minh.
Vì a lẻ nên \(a\ne0\), phương trình \(ax^2+bx+c=0\) là phương trình bậc hai.
Xét \(\Delta=b^2-4ac\): b lẻ, theo bài toán phụ có \(b^2=8k+1\left(k\in Z\right)\)
a,c lẻ \(\Rightarrow\) \(ac\) lẻ
Đặt \(ac=2l-1\left(l\in Z\right)\)
Do đó \(\Delta=b^2-4ac=8k+1-4.\left(2l-1\right)=8k+1-8l+4=8\left(k-l\right)+5 \)chia cho 8 dư 5, theo bài toán phụ trên ta có \(\Delta\) không phải số chính phương.
\(\Delta\) là số nguyên, không phải óố chính phương \(\Rightarrow\sqrt{\Delta}\) là số vô tỉ
Nghiệm của phương trình đã cho (nếu có) là: \(x=\frac{-b\pm\sqrt{\Delta}}{2a}\)
b,a\(\in Z\), \(\sqrt{\Delta}\) vô tỉ nên x là vô tỉ.
Vậy phương trình có nghiệm nếu có thì các nghiệm ấy không thể là số hữu tỉ.
ơng là phươngax2+bx+c=0

a) ĐK: x-1 khác 0 và x+1 khác 0
<=> x khác 1 và x khác -1
b) ĐK: x-2 khác 0
<=> x khác 2
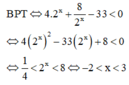
Đáp án D
Ta có:
2 x + 2 + 8.2 − x − 33 < 0 ⇔ 4.2 x + 8 2 x − 33 < 0 ⇔ 4. 2 x 2 − 33.2 x + 8 < 0 ⇔ 1 4 < 2 x < 8 ⇔ − 2 > x < 3