Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Bước 1: Biểu diễn diện tích x chiếc ghế và y chiếc bàn.
Diện tích của x chiếc ghế là \(0,5x\left( {{m^2}} \right)\) và y chiếc bàn là \(1,2y\left( {{m^2}} \right)\)
Bước 2: Biểu diễn diện tích lưu thông và cho lớn hơn hoặc bằng 12 \({m^2}\).
Tổng diện tích x chiếc ghế và y chiếc bàn là \(0,5x + 1,2y\left( {{m^2}} \right)\)
Diện tích lưu thông là \(60 - 0,5x - 1,2y\left( {{m^2}} \right)\)
Bất phương trình cần tìm là
\(\begin{array}{l}60 - 0,5x - 1,2y \ge 12\\ \Leftrightarrow 0,5x + 1,2y \le 48\end{array}\)
b)
+) Thay x=10, y=10 ta được
\(0,5.10 + 1,2.10 = 17 \le 48\)
=> (10;10) là nghiệm của bất phương trình
+) Thay x=10, y=20 ta được
\(0,5.10 + 1,2.20 = 29 \le 48\)
=> (10;20) là nghiệm của bất phương trình
+) Thay x=20, y=10 ta được
\(0,5.20 + 1,2.10 = 22 \le 48\)
=> (20;10) là nghiệm của bất phương trình
Chú ý
Ta có thể lấy các giá trị khác để thay vào, nếu thỏa mãn bất phương trình thì đó là nghiệm.

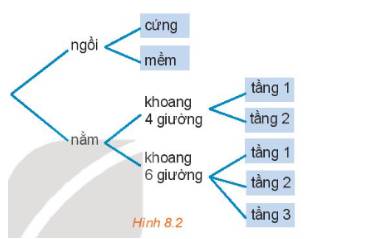
a) Số vé ghế ngồi là 2 (loại vé)
Số vé giường nằm là 2 + 3 = 5 (loại vé)
b) Số loại vé để bạn An lựa chọn là:
2 + 5 = 7 (loại vé)

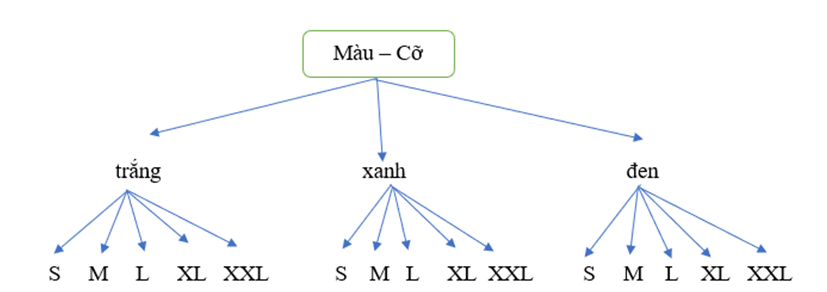
a) Cỡ áo: S, M, L, XL, XXL (5 loại cỡ).
Màu áo: trắng, xanh, đen (3 loại màu áo).
Ta có thể vẽ sơ đồ hình cây biểu thị các loại áo sơ mi với màu và cỡ áo nói trên như sau:
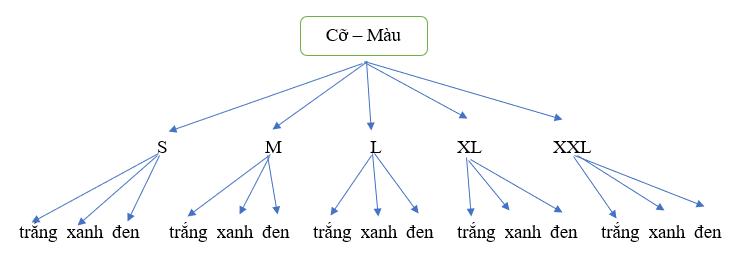
Hoặc ta cũng có thể vẽ sơ đồ cây trên dưới dạng sau:
b) Việc mua tất cả các loại áo sơ mi là việc thực hiện hai hành động liên tiếp: chọn màu áo và chọn cỡ áo.
+ Chọn màu áo: có 3 cách chọn.
+ Chọn cỡ áo: có 5 cách chọn.
Vậy cần mua tất cả 3 . 5 = 15 chiếc áo sơ mi.
Lưu ảnh về rồi tải lên bạn ơi chứ đừng copy nguyên ảnh như vậy.

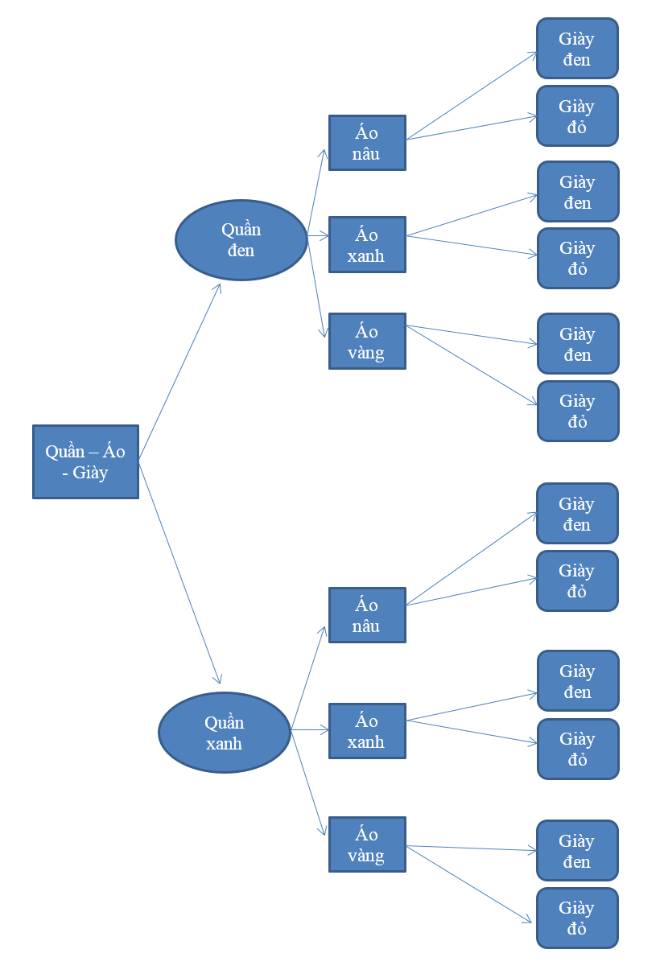
Kết luận: Từ sơ đồ cây, ta thấy bạn Dương có 12 cách chọn một bộ quần áo và một đôi giày.

Tham khảo:
a)
Bước 1: Ta có:
| Loại A | Loại B |
Giá mua vào | 10 triệu đồng/1 máy | 20 triệu đồng/1 máy |
Lợi nhuận | 2,5 triệu đồng/1 máy | 4 triệu đồng/1 máy |
Bước 2: Lập hệ bất phương trình
Vì số lượng máy là số tự nhiên nên ta có \(x \ge 0;y \ge 0\)
Vốn nhập vào x máy loại A và y máy loại B là \(10x + 20y\)(triệu đồng)
4 tỉ đồng=4000 (triệu đồng)
Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên ta có bất phương trình
\(10x + 20y \le 4000\) \( \Leftrightarrow x + 2y \le 400\)
Vì tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy nên ta có \(x + y \le 250\).
Vậy ta có hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + 2y \le 400\\x + y \le 250\end{array} \right.\)
Bước 3: Xác định miền nghiệm
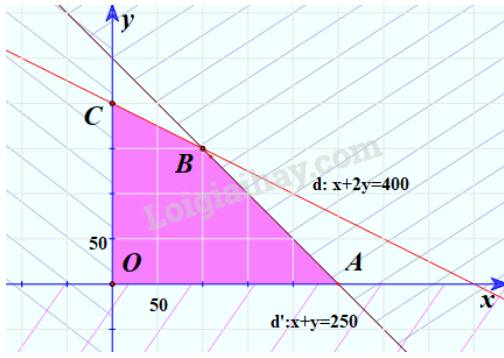
Miền nghiệm là tứ giác OABC với tọa độ các đỉnh này là O(0;0), A(250;0), B(100;150), C(0;200)
b) Lợi nhuận hàng tháng là F(x;y)=2,5x+4y(triệu đồng)
c) Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + 2y \le 400\\x + y \le 250\end{array} \right.\)
Ta có F(0;0)=0, F(250;0)=2,5.250+4.0=625
F(100;150)=2,5.100+4.150=850
F(0;200)=2,5.0+4.200=800
Giá trị lớn nhất là F(100;150)=850.
Vậy cửa hàng cần đầu tư kinh doanh 100 máy A và 150 máy B.
a) Số máy tính loại A cửa hàng cần nhập trong một tháng là x (máy), số máy tính loại B cửa hàng cần nhập trong một tháng là y (máy) (x,y≥0).
Do tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy: x + y ≤ 250
Tổng số vốn cửa hàng cần nhập hai loại A và B: 10x + 20y (triệu đồng)
Vì mỗi chiếc máy tính loại A có giá 10 triệu và mỗi máy tính loại B có giá 20 triệu nên tổng số vốn cửa hàng cần nhập hai loại A và B: 10x + 20y (triệu đồng)
Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên ta có: 10x + 20y ≤ 4 000 hay x + 2y ≤ 400.
Ta có hệ bất phương trình: \(\left\{{}\begin{matrix}x\ge0\\y\ge0\\x+y\le250\\x+2y\le400\end{matrix}\right.\)
Ta xác định miền nghiệm của hệ bất phương trình trên:
+) Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1;0).
+) Miền nghiệm D2 của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0;1).
+) Xác định miền nghiệm D3 của bất phương trình x + y ≤ 250.
- Vẽ đường thẳng d: x + y = 250.
- Vì 0 + 0 = 0 < 250 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + y ≤ 250
Do đó miền nghiệm D3 của bất phương trình x + y ≤ 250 là nửa mặt phẳng bờ d chứa gốc tọa độ.
+) Xác định miền nghiệm D4 của bất phương trình x + 2y ≤ 400.
- Vẽ đường thẳng d’: x + 2y = 400.
- Vì 0 + 2.0 = 0 < 400 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + 2y < 400
Do đó miền nghiệm D4 của bất phương trình x + 2y < 400 là nửa mặt phẳng bờ d’ chứa gốc tọa độ.
Miền nghiệm của hệ bất phương trình trên là tứ giác OABC với O(0;0), A(0; 200), C(100;150), B(250;0)
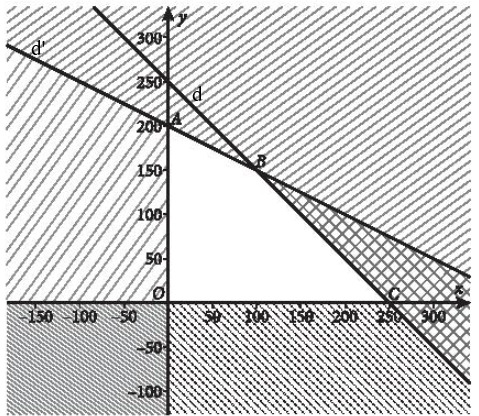
b) Lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B là: F(x;y) = 2,5x + 4y (triệu đồng).
Vậy F(x;y) = 2,5x + 4y.
c) Bài toán chuyển về tìm giá trị lớn nhất của F(x;y) với (x;y) thuộc miền nghiệm của hệ bất phương trình \(\left\{{}\begin{matrix}x\ge0\\y\ge0\\x+y\le250\\x+2y\le400\end{matrix}\right.\)
Người ta đã chứng minh được, giá trị F(x; y) lớn nhất tại (x; y) là tọa độ của một trong bốn đỉnh O; A; B; C.
Tại O(0; 0), ta có: F(0; 0) = 2,5 . 0 + 4 . 0 = 0;
Tại A(0; 200), ta có: F(0; 200) = 2,5 . 0 + 4 . 200 = 800;
Tại B(100; 150), ta có: F(100; 150) = 2,5 . 100 + 4 . 150 = 850;
Tại B(250; 0), ta có: F(250; 0) = 2,5 . 250 + 4 . 0 = 625.
Do đó F(x;y) lớn nhất bằng 850 tại x = 100 và y = 150.
Vậy cửa hàng cần nhập 100 máy loại A, 150 máy loại B để cửa hàng thu được lợi nhuận lớn nhất là 850 triệu đồng.

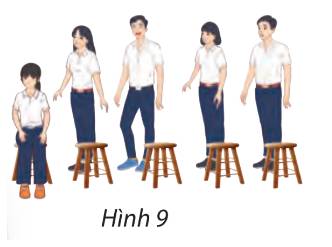
a) Mỗi cách sắp xếp 5 bạn học sinh vào 5 chiếc ghế là một hoán vị của 5 bạn học sinh. Do đó, số cách sắp xếp 5 bạn học sinh ngồi vào 5 cái ghế là hoán vị là:
\({P_5} = 5!\) (cách)
b) Khi bạn Nga nhất định ngồi vào chiếc ghế ngoài cùng bên trái, thì số cách sắp xếp là số cách sắp xếp 4 bạn còn lại vào 4 chiếc ghế, mỗi cách như vậy là một hoán vị của 4 bạn học sinh. Do đó, số cách sắp xếp là:
\({P_4} = 4! = 24\) (cách)
Số cách chọn là \(C^2_{35}=595\left(cách\right)\)