Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

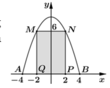
Chọn hệ trục tọa độ Oxy như hình vẽ.
Parabol đối xứng qua Oy nên có dạng ![]()
Vì (P) đi qua B(4;0) và N(2;6) nên ![]()
Diện tích hình phẳng giới hạn bởi (P) và trục Ox là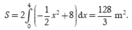
Diện tích phần trồng hoa là ![]()
Do đó số tiền cần dùng để mua hoa là ![]()
Chọn D.

Phương pháp:
+ Tìm phương trình Parabol
+ Diện tích hình phẳng giới hạn bởi
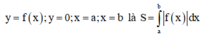
+ Tính diện tích hình chữ nhật từ đó tính diện tích phần trồng hoa và tính số tiền cần dùng để mua hoa trang trí.
Cách giải:
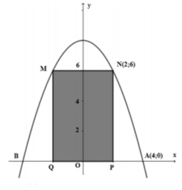
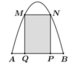
Gắn hệ trục tọa độ Oxy như hình vẽ, ta có Parabol đi qua các điểm A 4 ; 0 ; N 2 ; 6

Hoành độ giao điểm của Parabol và trục hoành là


Chọn B
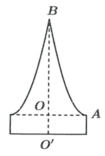
Chia mặt cắt của chiếc mũ làm hai phần:
● Phần dưới OA là hình chữ nhật có hai kích thước 5cm; 20cm
Quay hình chữ nhật quanh trục OO’, ta được khối trụ có R = OA = 10, h = OO' = 5
Do đó thể tích phần bên dưới là ![]()
● Phần trên OA là hình (H) giới hạn bởi đường cong AB, đường thẳng OA
Quay hình (H) quanh trục OB ta được phần thể tích bên trên
Dễ thấy parabol (P) có đỉnh A(10;0) và đi qua B(0;20)
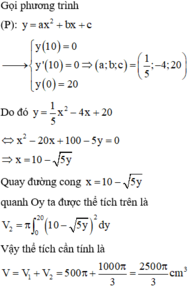

Gắn hệ trục tọa độ như sau:
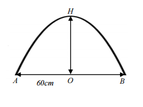
+) Gọi phương trình parapol là P : a x 2 + + b x + c
(P) đi qua A(1,00); B(0;2;0) và nhận x = 10 là trục đối xứng nên ta có hệ phương trình:


Thể tích khối tròn xoay giới hạn bởi (P), trục Ox, Oy là

+) Thể tích khối trụ có chiều cao h = 5

Chọn B.

Cho tam giác ABC đều
D thuộc AB , E thuộc AC sao cho BD = AE
CM : Khi D,E thay đổi ( di chuyển ) trên AB,AC thì đường trung tuyến DE luôn đi qua điểm cố định
Help me !!!

Đáp án A
Ycbt ⇔ đường thẳng d đi qua điểm uốn của đồ thị C (*)
Ta có:
f ' x = 3 x 2 − 6 x ⇒ f ' ' x = 6 x − 6 = 0 ⇔ x = 1
suy ra điểm uốn I 1 ; − 3
Do đó * ⇔ − 3 = 1 + m ⇔ m = − 4 ∈ − 5 ; − 3



Đáp án B
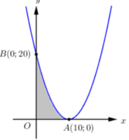
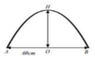
Đặt hệ trục tọa độ với Oxy với tia Ox là tia OH, tia Oy là tia OB
Giả sử phương trình parabol y = f x = a x 2 + b x + c .
Dựa vào AB = 60 cm, OH = 30 cm
Ta có f ± 30 = 0 f 0 = 30 ⇒ a = - 1 30 , b = 0 , c = 30 ⇒ y = f x = - 1 30 x 2 + 30
Diện tích chiếc gương là S = ∫ - 30 30 f ( x ) d x = ∫ - 30 30 - 1 30 x 2 + 30 d x = - 1 30 x 2 + 30 - 30 30 = 1200 c m 2