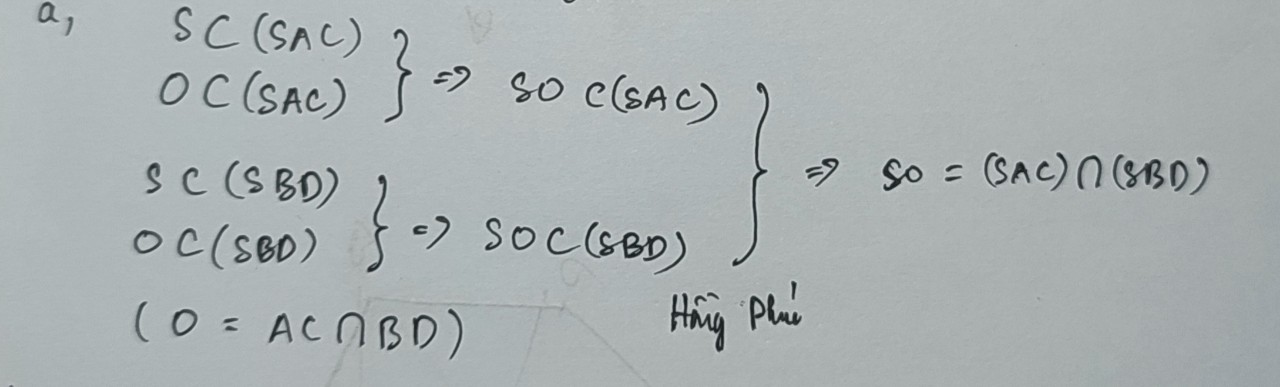Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
a, Phương trình có nghiệm khi:
\(\left(m+2\right)^2+m^2\ge4\)
\(\Leftrightarrow m^2+4m+4+m^2\ge4\)
\(\Leftrightarrow2m^2+4m\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}m\ge0\\m\le-2\end{matrix}\right.\)
b, Phương trình có nghiệm khi:
\(m^2+\left(m-1\right)^2\ge\left(2m+1\right)^2\)
\(\Leftrightarrow2m^2+6m\le0\)
\(\Leftrightarrow-3\le m\le0\)
2.
a, Phương trình vô nghiệm khi:
\(\left(2m-1\right)^2+\left(m-1\right)^2< \left(m-3\right)^2\)
\(\Leftrightarrow4m^2-4m+1+m^2-2m+1< m^2-6m+9\)
\(\Leftrightarrow4m^2-7< 0\)
\(\Leftrightarrow-\dfrac{\sqrt{7}}{2}< m< \dfrac{\sqrt{7}}{2}\)
b, \(2sinx+cosx=m\left(sinx-2cosx+3\right)\)
\(\Leftrightarrow\left(m-2\right)sinx-\left(2m+1\right)cosx=-3m\)
Phương trình vô nghiệm khi:
\(\left(m-2\right)^2+\left(2m+1\right)^2< 9m^2\)
\(\Leftrightarrow m^2-4m+4+4m^2+4m+1< 9m^2\)
\(\Leftrightarrow m^2-1>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)

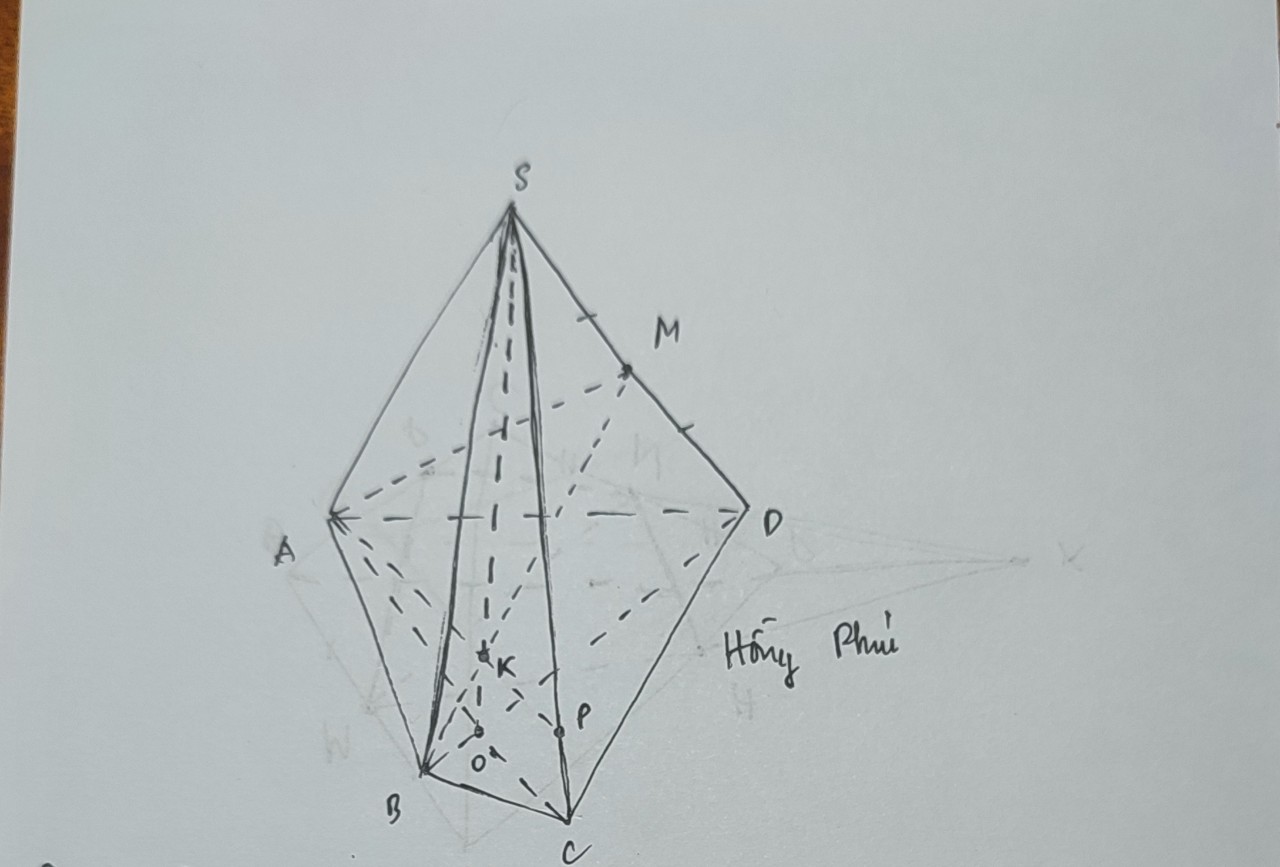
a: Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Gọi K là giao điểm của AB và CD
\(K\in AB\subset\left(SAB\right)\)
\(K\in CD\subset\left(SCD\right)\)
Do đó: \(K\in\left(SAB\right)\cap\left(SCD\right)\)
mà \(S\in\left(SAB\right)\cap\left(SCD\right)\)
nên \(\left(SAB\right)\cap\left(SCD\right)=SK\)
b: Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
c: Chọn mp(SCD) có chứa CD
\(N\in SC\subset\left(SCD\right)\)
\(P\in SD\subset\left(SCD\right)\)
Do đó: \(NP\subset\left(SCD\right)\)
mà \(NP\subset\left(MNP\right)\)
nên (SCD) giao (MNP)=NP
Gọi E là giao điểm của CD với NP
=>E là giao điểm của CD với (MNP)
Chọn mp(SBD) có chứa MP
\(BD\subset\left(SBD\right)\)
\(BD\subset\left(ABCD\right)\)
Do đó: \(BD\subset\left(SBD\right)\cap\left(ABCD\right)\)
Gọi F là giao điểm của MP với BD
=>F là giao điểm của MP với (ABCD)

c/
\(\Leftrightarrow\frac{1}{2}sin2x-\frac{\sqrt{3}}{2}cos2x=\frac{\sqrt{3}}{2}sinx+\frac{1}{2}cosx\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{3}\right)=sin\left(x+\frac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=x+\frac{\pi}{6}+k2\pi\\2x-\frac{\pi}{3}=\frac{5\pi}{6}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k2\pi\\x=\frac{7\pi}{18}+\frac{k2\pi}{3}\end{matrix}\right.\)
2.
Theo điều kiện có nghiệm của pt lượng giác bậc nhất với sin và cos:
\(m^2+\left(m-1\right)^2\ge5\)
\(\Leftrightarrow m^2-m-2\ge0\Leftrightarrow\left[{}\begin{matrix}m\ge2\\m\le-1\end{matrix}\right.\)
a/
\(\Leftrightarrow\sqrt{2}sin\left(x-\frac{\pi}{4}\right)=\sqrt{3}\)
\(\Leftrightarrow sin\left(x-\frac{\pi}{4}\right)=\sqrt{\frac{3}{2}}>1\)
Pt vô nghiệm
b/
\(\Leftrightarrow\frac{2}{\sqrt{13}}sinx+\frac{3}{\sqrt{13}}cosx=\frac{2}{\sqrt{13}}\)
Đặt \(\frac{2}{\sqrt{13}}=cosa\) với \(a\in\left(0;\pi\right)\)
\(\Rightarrow sinx.cosa+cosx.sina=cosa\)
\(\Leftrightarrow sin\left(x+a\right)=sin\left(\frac{\pi}{2}-a\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x+a=\frac{\pi}{2}-a+k2\pi\\x+a=\frac{\pi}{2}+a+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}-2a+k2\pi\\x=\frac{\pi}{2}+k2\pi\end{matrix}\right.\)

a) làm tương tự 2 bài mk đã giải nha.
b) \(y=2\cos^2x-2\sqrt{3}\sin x\cos x+1\)
\(=1-\left(\cos2x+\sqrt{3}\sin2x\right)\)
Lại có \(-2\le\cos2x+\sqrt{3}\sin2x\le2\) \(\Rightarrow-1\le y\le3\)
c) Vì \(\left\{{}\begin{matrix}0\le\sqrt[4]{\sin x}\le1\\0\le\sqrt{\cos x}\le1\end{matrix}\right.\)
Do đó \(-1\le y\le1\)

3.
Gọi số đó là \(\overline{abcdef}\)
- Nếu \(f>6\Rightarrow f\) có 2 cách chọn (7,9)
\(a\) có 5 cách chọn, 4 số còn lại có \(A_8^4\) cách
\(\Rightarrow2.5.A_8^4\) số
- Nếu \(f< 6\Rightarrow f\) có 3 cách chọn
a có 4 cách chọn, 4 số còn lại có \(A_8^4\) cách chọn
\(\Rightarrow3.4.A_8^4\) số
Vậy tổng cộng có: \(2.5.A_8^4+3.4.A_8^4=...\) số thỏa mãn
\(\Leftrightarrow\left(2cosx-sinx\right)\left(1+sinx\right)=1-sin^2x\)
\(\Leftrightarrow\left(2cosx-sinx\right)\left(1+sinx\right)=\left(1+sinx\right)\left(1-sinx\right)\)
\(\Leftrightarrow\left(1+sinx\right)\left(2cosx-sinx-1+sinx\right)=0\)
\(\Leftrightarrow\left(1+sinx\right)\left(2cosx+1\right)=0\)
\(\Leftrightarrow...\)
2.
Gọi số đó là \(\overline{abc}\)
- TH1: \(a=3\) \(\Rightarrow b\le4\)
+ Nếu \(b=4\Rightarrow c\) có 1 cách chọn (5)
+ Nếu \(b< 4\Rightarrow b\) có 2 cách chọn (1;2), c có 4 cách chọn
\(\Rightarrow1+2.4=9\) số
- TH2: \(a< 3\Rightarrow a\) có 2 cách chọn
Bộ bc có \(A_5^2=20\) cách chọn
Vậy có: \(9+2.20=49\) số

a) ĐS: 4 số.
b) Số tự nhiên cần lập có dạng , với a, b ∈ {1, 2, 3, 4} có kể đến thứ tự.
Để lập được số tự nhiên này, phải thực hiện liên tiếp hai hành động sau đây:
Hành động 1: Chọn chữ số a ở hàng chục. Có 4 cách để thực hiện hành động này
Hành động 2: Chọn chữ số b ở hàng đơn vị. Có 4 cách để thực hiện hành động này.
Theo quy tắc nhân suy ra số các cách để lập được số tự nhiên kể trên là
4 . 4 = 16 (cách).
Qua trên suy ra từ các chữ số đã cho có thể lập được 16 số tự nhiên có hai chữ số.
c) Số tự nhiên cần lập có dạng , với a, b ∈ {1, 2, 3, 4} và a, b phải khác nhau, có kể đến thứ tự.
Để lập được số tự nhiên này, phải thực hiện liên tiếp hai hành động sau đây:
Hành động 1: Chọn chữ số a ở hàng chục.
Có 4 cách để thực hiện hành động này.
Hành động 2: Chọn chữ số b ở hàng đơn vị, với b khác chữ số a đã chọn.
Có 3 cách để thực hiện hành động này.
Theo quy tắc nhân suy ra từ các cách để lập được số tự nhiên kể trên là:
4 . 3 = 12 (cách).
Qua trên suy ra từ các chữ số đã cho có thể lập được 12 số tự nhiên có hai chữ số khác nhau.