Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{1993+1993.1994}{1992.1995+1995}\)
=\(\dfrac{1993.1+1993.1994}{1992.1995+1995.1}\)
=\(\dfrac{1993\left(1+1994\right)}{1995\left(1992+1\right)}\)
=\(\dfrac{1993.1995}{1995.1993}\)
=1
\(=\dfrac{1993.1+1993.1994}{1992.1995+1995.1}\)
\(=\dfrac{1993\left(1+1994\right)}{1995\left(1992+1\right)}\)
\(=\dfrac{1993.1995}{1995.1993}\)
=1

Tính nhanh :
A = \(2016.20152015-2015.20162016\)
= \(2016.2015.10001-2015.2016.1001\)
=0
\(A=2016.20152015-2015.20162016\)
\(=2016.2015.10001-2015.2016.10001\)
\(=0\)

Áp dụng tính chất phân phối, rồi tính giá trị biểu thức.
Chẳng hạn,
Với , thì
ĐS. ; C = 0.
Xem thêm tại: http://loigiaihay.com/bai-77-trang-39-phan-so-hoc-sgk-toan-6-tap-2-c41a5943.html#ixzz4eU1fQCGw

F=(9.75.21\(\dfrac{3}{7}\)+\(\dfrac{39}{4}\).18\(\dfrac{4}{7}\)).\(\dfrac{15}{78}\)
=(\(\dfrac{39}{4}\).21\(\dfrac{3}{7}\)+\(\dfrac{39}{4}\).18\(\dfrac{4}{7}\)).\(\dfrac{15}{78}\)
=[\(\dfrac{39}{4}\).(21\(\dfrac{3}{7}\)+18\(\dfrac{4}{7}\))].\(\dfrac{15}{78}\)
=[\(\dfrac{39}{4}\).(21+18)+(\(\dfrac{3}{7}\)+\(\dfrac{4}{7}\))].\(\dfrac{15}{78}\)
=[\(\dfrac{39}{4}\).(39+1)].\(\dfrac{15}{78}\)
=(\(\dfrac{39}{4}\).40).\(\dfrac{15}{78}\)
=390.\(\dfrac{15}{78}\)=75
\(B=71\dfrac{38}{45}-\left(43\dfrac{8}{45}-1\dfrac{17}{57}\right)\)
\(B=71\dfrac{38}{45}-43\dfrac{8}{45}-1\dfrac{17}{57}\)
\(B=28\dfrac{2}{3}-1\dfrac{17}{57}=27\dfrac{11}{57}\)
\(D=\left(19\dfrac{5}{8}:\dfrac{7}{12}-13\dfrac{1}{4}:\dfrac{7}{12}\right).\dfrac{4}{5}\)
\(D=\dfrac{12}{7}.\left(19\dfrac{5}{8}-13\dfrac{1}{4}\right).\dfrac{4}{5}\)
\(D=\dfrac{12}{7}.\dfrac{51}{8}.\dfrac{4}{5}=\dfrac{306}{35}\)
Câu còn lại làm tương tự!
Chúc bạn học tốt!!!

Gợi ý: Sử dụng tính chất phân phối của phép nhân đối với phép cộng để nhóm thừa số chung ra ngoài.

\(A=\dfrac{1995.1994-1}{1993.1995+1994}=\dfrac{1995\left(1993+1\right)-1}{1993.1995+1994}=\dfrac{1995.1993+1995-1}{1993.1995+1994}=\dfrac{1995.1993+1994}{1995.1993-1994}=1\)\(B=\dfrac{2004.2004+3006}{2005.2005-1003}=\dfrac{2004.2004+2004.1+1002}{2005.2005-1003}=\dfrac{2004.2005+1002}{2005.2005-1003}=\dfrac{2004.2005+1002}{2004.2005+2005-1003}=\dfrac{2004.2005+1002}{2004.2005+1002}=1\)\(C=\dfrac{2010.2011-1}{2009.2011+2010}=\dfrac{2009.2011+2011-1}{2009.2011+2010}=\dfrac{2019.2011+2010}{2009.20011+2010}=1\)\(D=\dfrac{2014.2015-1}{2013.2015+2013}=\dfrac{2013.2015+2014-1}{2013.2015+2013}=\dfrac{2013.2015+2013}{2013.2015+2013}=1\)
Câu 1 nhầm đề nha bạn mình sửa:
\(\dfrac{1995.1994-1}{1993.1995+1994}\)
\(=\dfrac{1995.\left(1993+1\right)-1}{1993.1995+1994}\)
\(=\dfrac{1995.1993+1995-1}{1993.1995+1994}\)
\(=\dfrac{1993.1995+1994}{1993.1995+1994}\)
\(=1\)
Câu 2: \(\dfrac{2004.2004+3006}{2005.2005-1003}\)
\(=\dfrac{2004.2004+2004+1002}{\left(2004+1\right).\left(2004+1\right)-1003}\)
\(=\dfrac{2004.2004+2004+1002}{2004.2004+2004+1-1003}\)
\(=\dfrac{2004.2004+2004+1002}{2004.2004+2004+1002}\)
\(=1\)
Câu 3:\(\dfrac{2010.2011-1}{2009.2011+2010}\)
\(=\dfrac{\left(2009+1\right).2011-1}{2009.2011+2010}\)
\(=\dfrac{2009.2011+2011-1}{2009.2011+2010}\)
\(=\dfrac{2009.2011+2010}{2009.2011+2010}\)
= 1
Câu 4:Nhầm để, sửa:
\(\dfrac{2014.2015-1}{2013.2015+2014}\)
\(=\dfrac{\left(2013+1\right).2015-1}{2013.2015+2014}\)
\(=\dfrac{2013.2015+2015-1}{2013.2015+2014}\)
\(=\dfrac{2013.2015+2014}{2013.2015+2014}\)
\(=1\)

A= \(\dfrac{-3}{5}-\dfrac{-4}{5}+\dfrac{-9}{10}\)
A = \(\dfrac{-7}{10}\)

B=\(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}\)
B=\(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}\)
B=\(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}\)
B= 1-\(\dfrac{1}{8}\)
B= \(\dfrac{7}{8}\)
\(A=\dfrac{5}{9}-\dfrac{5}{8}+\dfrac{2}{3}+\dfrac{4}{9}+\dfrac{-3}{8}+\dfrac{1}{3}\\ =\dfrac{5}{9}+\dfrac{-5}{8}+\dfrac{2}{3}+\dfrac{4}{9}+\dfrac{-3}{8}+\dfrac{1}{3}\\= \left(\dfrac{5}{9}+\dfrac{4}{9}\right)+\left(\dfrac{2}{3}+\dfrac{1}{3}\right)+\left(\dfrac{-5}{8}+\dfrac{-3}{8}\right)\\ =1+1+\left(-1\right)\\ =2+\left(-1\right)\\ =1\)

3. Gọi d là ƯCLN(2n + 3, 4n + 8), d ∈ N*
\(\Rightarrow\hept{\begin{cases}2n+3⋮d\\4n+8⋮d\end{cases}\Rightarrow\hept{\begin{cases}2\left(2n+3\right)⋮d\\4n+8⋮d\end{cases}\Rightarrow}\hept{\begin{cases}4n+6⋮d\\4n+8⋮d\end{cases}}}\)
\(\Rightarrow\left(4n+8\right)-\left(4n+6\right)⋮d\)
\(\Rightarrow2⋮d\)
\(\Rightarrow d\in\left\{1;2\right\}\)
Mà 2n + 3 không chia hết cho 2
\(\Rightarrow d=1\)
\(\RightarrowƯCLN\left(2n+3,4n+8\right)=1\)
\(\Rightarrow\frac{2n+3}{4n+8}\) là phân số tối giản.
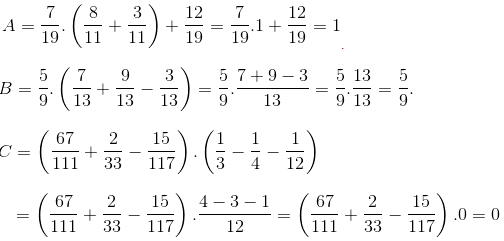
A= \(\dfrac{1993\left(1994+1\right)}{1995\left(1992+1\right)}\)=1
B=\(\dfrac{399\left(45+55\right)}{1995\left(1996-1991\right)}\)=\(\dfrac{399.5.100}{399.5.5}\)=100