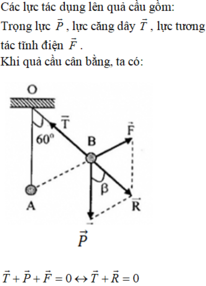
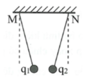
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Na ná bài hôm nay tui thi luôn :v
\(F=\dfrac{kq_1q_2}{r^2}\)
Sau khi tiếp xúc, điện tích 2 quả cầu bằng nhau: \(q=\dfrac{\left(q_1+q_2\right)}{2}\Rightarrow F'=\dfrac{k\left(\dfrac{q_1+q_2}{2}\right)^2}{r'^2}=\dfrac{k\left(q_1+q_2\right)^2}{4r'^2}\)
Gọi alpha là góc hợp bởi dây với phương thẳng đứng lúc chưa tiếp xúc, alpha rất nhỏ=> \(\tan\alpha=\sin\alpha=\dfrac{r}{2l}\) \(\Rightarrow r=2l.\tan\alpha\)
\(\tan\alpha=\dfrac{F}{P}\Rightarrow\tan\alpha=\dfrac{kq_1q_2}{r^2.P}=\dfrac{kq_1q_2}{\tan^2\alpha.4l^2.P}\Rightarrow\tan^3\alpha=\dfrac{kq_1q_2}{4l^2.P}\)
Gọi alpha phẩy là góc hợp bởi dây với phương thẳng đứng sau khi tiếp xúc
\(\Rightarrow r'=2l\tan\alpha'\Rightarrow\tan^3\alpha'=\dfrac{k\left(\dfrac{q_1+q_2}{2}\right)^2}{4l^2.P}\)
\(\Rightarrow\dfrac{\tan^3\alpha}{\tan^3\alpha'}=\dfrac{\dfrac{kq_1q_2}{4l^2.P}}{\dfrac{k\left(\dfrac{q_1+q_2}{2}\right)^2}{4l^2.P}}=\dfrac{4q_1q_2}{\left(q_1+q_2\right)^2}\)
Ta luôn có \(\left(q_1+q_2\right)^2\ge4q_1q_2\Rightarrow"="\Leftrightarrow q_1=q_2\Leftrightarrow\alpha=\alpha'\Leftrightarrow r'=r\)

P Fđ T α
$a)$ Ở đây điện tích của mỗi quả cầu $\dfrac{q}{2} $ (vì hai quả cầu giống nhau)
Ta có công thức tính góc lệch $\alpha $:
$\tan \alpha =\dfrac{F_đ}{P} =\frac{k(\dfrac{q}{2} )^2}{mga^2} (1)$
Vì góc lệch $\alpha $ rất nhỏ nên $\tan \alpha \approx \sin \alpha \approx \dfrac{\dfrac{a}{2} }{l} =\dfrac{a}{2l} (2)$
Từ $(1),(2) $ ta có : $\dfrac{a}{2l}=\dfrac{kp^2}{4mga^2} $ suy ra $a^3=\dfrac{kq^2l}{2mg} $
Thay số vào ta được : $a=6.10^{-2}m=6cm$
$b)$ Khi có một trong hai quả cầu bị mất hết điện tích, không có lực điện tương tác giữa hai quả cầu, do đó chúng trở về vị trí cân bằng theo phương thẳng đứng (dây treo không bị lệch) và tại đó chúng chạm vào nhau.Khi đó điện tích của quả cầu kia (bằng $\dfrac{q}{2} $) lại được phân bố lại cho cả hai quả cầu, và do đó mỗi quả cầu sẽ có điện tích $\dfrac{q}{4} $ : hai quả cầu lại đẩy nhau ra xa và khoảng cách giữa chúng bây giờ là $b$.Lập luận hoàn toàn tương tự như trên, với chú ý rằng điện tích của mỗi quả cầu bây giờ là $\dfrac{q}{4} $ ta sẽ được :
$b^3=\frac{kq^2l}{8mg} =\frac{a^3}{4} \Rightarrow b=(54)^{\frac{1}{3} }\approx 3,78 cm$

Góc lệch \(\alpha\) của dây treo được xác định bằng hệ thức (suy từ điều kiện cân bằng của hai quả cầu :)
\(\tan\alpha=\frac{F_đ}{P}\)
Với \(F_đ=k\frac{q^2}{a^2}\) Như vậy \(\tan\alpha=\frac{kq^2}{mga^2}\)
Thay số ta được : \(\tan\alpha=1\) suy ra \(\alpha=45^o\)
mình chưa hiểu đoạn tan a = F/P lắm bạn giải thích lại hộ mình đc ko

Chọn đáp án B
Góc lệch của mỗi quả cầu so với phương thẳng đứng được xác định bởi công thức


| 1Bình chọn giảm |
Xét quả cầu bị lệch chịu tác dụng của 2 lực, trong lực, lực căng dây và lực tĩnh điễn. Xét trục tọa độ sao cho trục y song song với dây và trục x vuông góc với dây Xét theo phương x thì mgsinα=Fcos(α/2)mgsinα=Fcos(α/2) vì 2 dây bằng nhau mgsin60=Fcos30mgsin60=Fcos30 mg=F=kq2r2mg=F=kq2r2 r=2lsin(α/2)r=2lsin(α/2) q2=mg4l2sin2(α/2)/kq2=mg4l2sin2(α/2)/k q=1.10−6Cq=1.10−6C |