
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
\(175\cdot19+38\cdot175+43\cdot175\\ =175\cdot19+175\cdot38+175\cdot43\\ =175\cdot\left(19+38+43\right)\\ =175\cdot100\\ =17500\)
b)
\(125\cdot75+125\cdot13-80\cdot125\\ =125\cdot75+125\cdot13-125\cdot80\\ =125\cdot\left(75+13-80\right)\\ =125\cdot10\\ =125\cdot8\\ =1000\)
a, 175. 19 + 38. 175 + 43. 175
= 175. 19 + 175. 38 + 175. 43
= 175.(19 + 38 + 43)
= 175. 100
= 17500


Lời giải:
a.
$=\frac{3}{5}-\frac{7}{4}=\frac{12-35}{20}=\frac{-23}{20}$
b.
$=-(2+\frac{5}{8})=-\frac{21}{8}$
c.
$=-(\frac{1}{8}+\frac{5}{9})=-\frac{9+8.5}{8.9}=\frac{-49}{72}$
d.
$=\frac{6}{13}-\frac{14}{39}=\frac{18}{39}-\frac{14}{39}=\frac{4}{39}$
e.
$=\frac{-3}{4}+\frac{5}{7}=\frac{5}{7}-\frac{3}{4}$
$=\frac{20-21}{7.4}=\frac{-1}{28}$

Bài 5
1) x ∈ Ư(18) = {1; 2; 3; 6; 9; 18}
x ∈ B(4) = {0; 4; 8; 12; 16; 20; ...}
Vậy không tìm được x thỏa mãn đề bài
2) x ∈ Ư(20) = {1; 2; 4; 5; 10; 20}
x ∈ B(2) = {0; 2; 4; 6; 8; 10; 12; 14; 16; 18; 20; ...}
⇒ x ∈ {2; 4; 10; 20}
3) x ∈ B(12) = {0; 12; 24; 36; 48; ...; 96; 108; ...}
Mà 30 ≤ x ≤ 100
⇒ x ∈ {36; 48; ...; 96}
4) x ∈ Ư(150) = {1; 2; 3; 5; 6; 10; 15; 25; 30; 50; 75; 150}
Mà x ≤ 50
⇒ x ∈ {1; 2; 3; 5; 6; 10; 15; 25; 30; 50}
5) 70 ⋮ x và 168 ⋮ x
⇒ x ∈ ƯC(70; 168)
Ta có:
70 = 2.5.7
168 = 2³.3.7
⇒ ƯCLN(70; 168) = 2.7 = 14
⇒ x ∈ ƯC(70; 168) = Ư(14) = {1; 2; 7; 14}
Mà x > 10
⇒ x = 14
6) Ta có:
(1995 + 2005 + x) ⋮ 5
1995 ⋮ 5
2005 ⋮ 5
⇒ x ⋮ 5
⇒ x ∈ B(5) = {0; 5; 10; 15; 20; 25; 30; 35; 40; ...}
Mà 23 < x ≤ 35
⇒ x ∈ {25; 30; 35}
Bài 6
1) Do 17x2y chia hết cho 2 và 5 nên y = 0
⇒ Số đã cho có dạng: 17x20
Để 17x20 chia hết cho 3 thì (1 + 7 + x + 2 + 0) ⋮ 3
⇒ (10 + x) ⋮ 3
⇒ x ∈ {2; 5; 8}
Vậy x ∈ {2; 5; 8}; y = 0
2) Do 234xy chia hết cho 2 và 5 nên y = 0
⇒ Số đã cho có dạng: 234x0
Để 234x0 chia hết cho 9 thì (2 + 3 + 4 + x + 0) ⋮ 9
⇒ (9 + x) ⋮ 9
⇒ x ∈ {0; 9}
Vậy x ∈ {0; 9}; y = 0
3) Do 4x6y chia hết cho 2 và 5 nên y = 0
Mà x - y = 4
⇒ x = 4 + y
⇒ x = 4
Vậy x = 4; y = 0
4) Do 57x2y chia hết cho 5 nhưng không chia hết cho 2 nên y = 5
⇒ Số đã cho có dạng 57x25
Để 57x25 chia hết cho 9 thì (5 + 7 + x + 2 + 5) ⋮ 9
⇒ (19 + x) ⋮ 9
⇒ x = 8
Vậy x = 8; y = 5


\(a,-\dfrac{5}{7}+1+\dfrac{30}{-7}\le x\le-\dfrac{1}{6}+\dfrac{1}{3}+\dfrac{5}{6}\\ \dfrac{-5+1.7-30}{7}\le x\le\dfrac{-1+1.2+5}{6}\\ -\dfrac{28}{7}\le x\le\dfrac{6}{6}\\ -4\le x\le1\\ Vậy:x\in\left\{-4;-3;-2;-1;0;1\right\}\)
\(b,\dfrac{-8}{13}+\dfrac{7}{17}+\dfrac{21}{13}\le x\le-\dfrac{9}{14}+3+\dfrac{5}{-14}\\ \left(\dfrac{21}{13}-\dfrac{8}{13}\right)+\dfrac{7}{17}\le x\le\left(-\dfrac{9}{14}-\dfrac{5}{14}\right)+3\\ 1+\dfrac{7}{17}\le x\le-1+3\\ 1\dfrac{7}{17}\le x\le2\\ Vậy:x=2\)

Lời giải:
$\frac{1}{50}> \frac{1}{100}$
$\frac{1}{51}> \frac{1}{100}$
.....
$\frac{1}{98}> \frac{1}{100}$
$\frac{1}{99}> \frac{1}{100}$
$\Rightarrow S> \underbrace{\frac{1}{100}+\frac{1}{100}+...+\frac{1}{100}}_{50}=\frac{1}{100}.50=\frac{1}{2}$

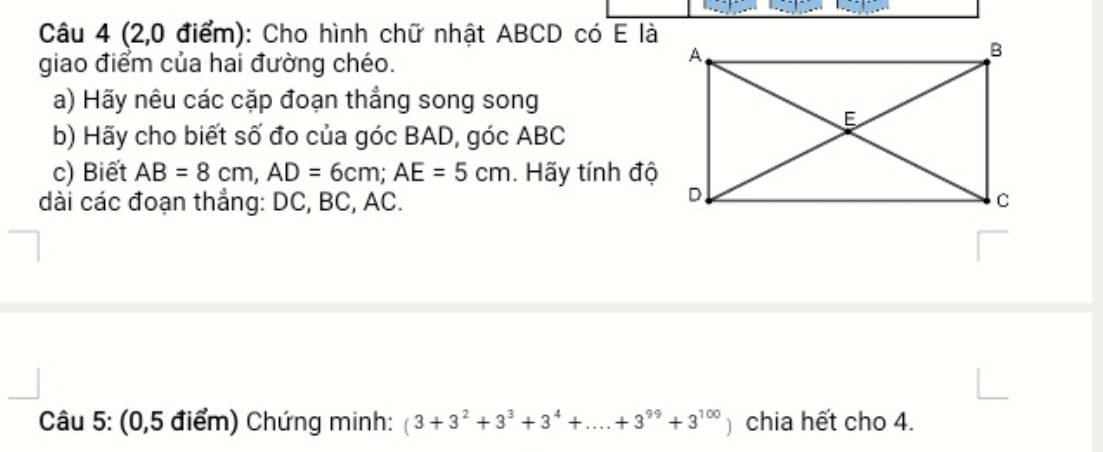
\(\left(3+3^2+3^3+3^4+...+3^{99}+3^{100}\right)\\ =3.\left(1+3\right)+3^3\left(1+3\right)+...+3^{99}\left(1+3\right)\\ =3.4+3^3.4+...+3^{99}.4\\ =4.\left(3+3^3+...+3^{99}\right)⋮4\left(ĐPCM\right)\)

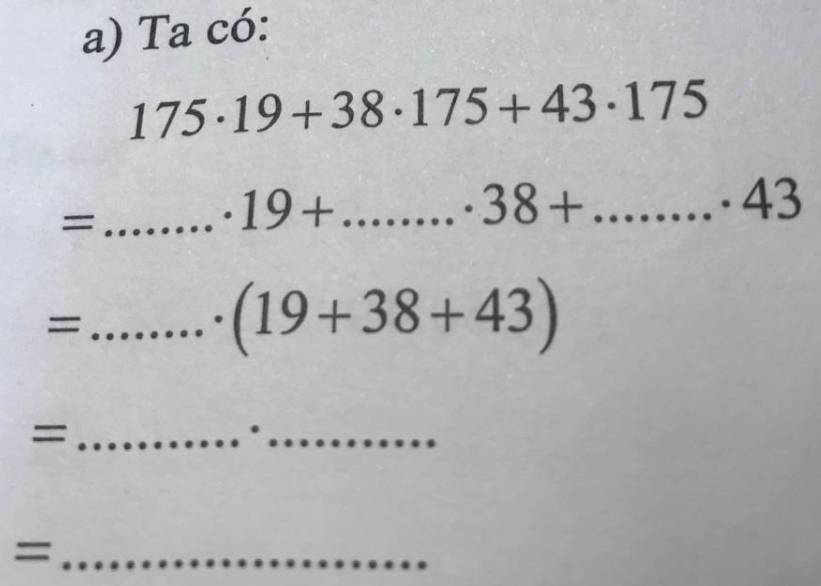
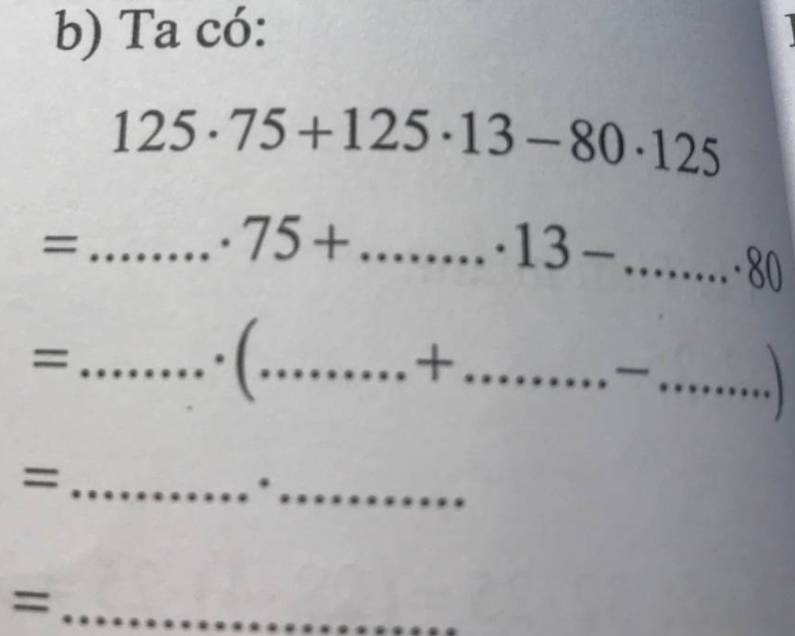
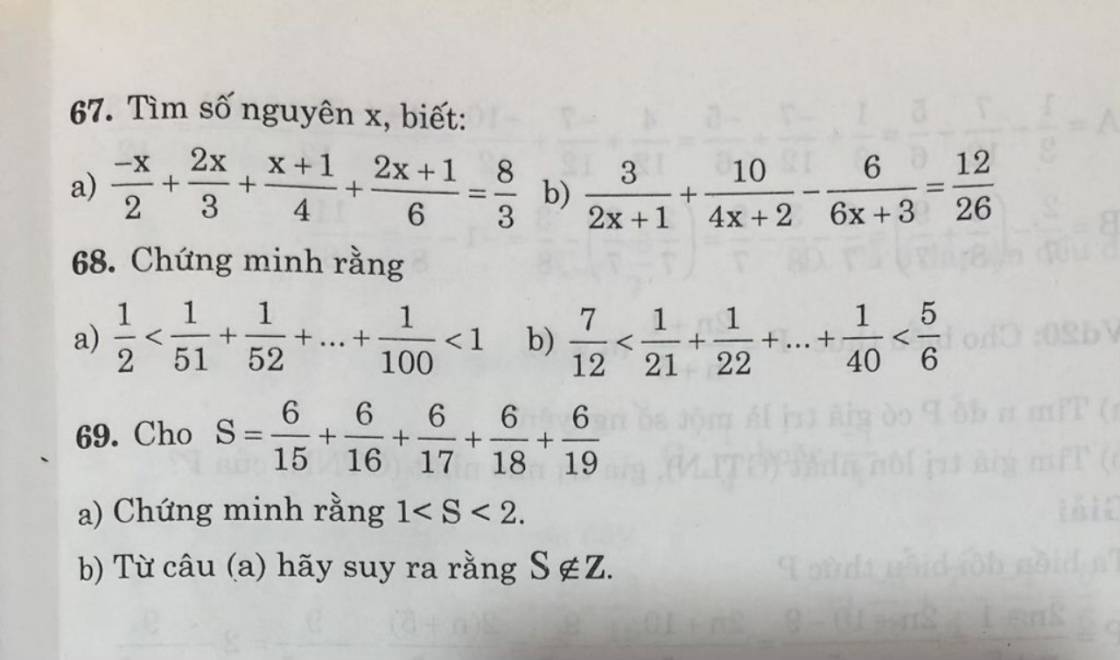
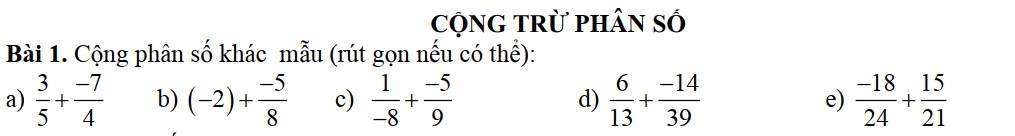

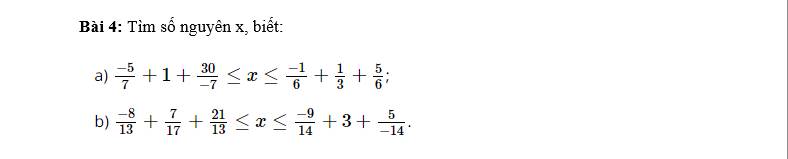

\(\left(a\right):\left(2^{17}+17^2\right).\left(9^{15}-3^{15}\right).\left(2^4-4^2\right)\\ =\left(2^{17}+17^2\right).\left(9^{15}-3^{15}\right).\left[2^4-\left(2^2\right)^2\right]\\ =\left(2^{17}+17^2\right).\left(9^{15}-3^{15}\right).\left(2^{2.2}-2^{2.2}\right)\\ =\left(2^{17}+17^2\right).\left(9^{15}-3^{15}\right).0=0\)
\(\left(b\right):\left(8^{2017}-8^{2015}\right):\left(8^{2104}.8\right)\\ =\dfrac{8^{2015}.\left(8^2-1\right)}{8^{2104+1}}\\ =\dfrac{8^{2015}.63}{8^{2105}}=\dfrac{63}{8^{90}}\)
\(\left(c\right):\left(1^3+2^3+3^4+5^5\right).\left(1^3+2^3+3^3+4^3\right).\left(3^8-81^2\right)\\ =\left(1^3+2^3+3^4+5^5\right).\left(1^3+2^3+3^3+4^3\right).\left[3^8-\left(3^4\right)^2\right]\\ =\left(1^3+2^3+3^4+5^5\right).\left(1^3+2^3+3^3+4^3\right).\left(3^{4.2}-3^{4.2}\right)\\ =\left(1^3+2^3+3^4+5^5\right).\left(1^3+2^3+3^3+4^3\right).0=0\)
\(\left(d\right):\left(2^8+8^3\right):\left(2^5.2^3\right)\\ =\dfrac{2^8+\left(2^3\right)^3}{2^5.2^3}\\ =\dfrac{2^8+2^9}{2^{5+3}}\\ =\dfrac{2^8.\left(1+2\right)}{2^8}=3\)
3