Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1, Gọi các cạnh của tam giác lần lượt là a,b,c
Ta có : \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\) và \(a+b+c=45\)
Theo tính chất dãy tỉ số bằng nhau, ta có :
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a+b+c}{2+3+4}=\frac{45}{9}=5\)
\(\Rightarrow\) \(a=10;b=15;c=20\)

Gọi số tiền lãi mà ba đơn vị được chia là x, y, z
Theo đề bài ta có:
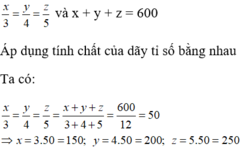
Chọn đáp án D

Gọi số tiền lãi mỗi đơn vị kinh doanh nhận được lần lượt là a,b,c ( triệu đồng ) ( 0 <a,b,c < 600 )
Theo bài ra ta có : \(\frac{a}{2}=\frac{b}{4}=\frac{c}{6}=\frac{a+b+c}{2+4+6}=\frac{600}{12}=50\)
\(=>\hept{\begin{cases}a=2.50=100\left(TM\right)\\b=4.50=200\left(TM\right)\\c=6.50=300\left(TM\right)\end{cases}}\)
Vậy ...

Gọi a,b,c (triệu đồng) lần lượt là số tiền lãi của 3 đơn vị (0 < a, b, c < 450).
Tổng số tiền lãi là 450 triệu đồng nên a+b+c = 450
Vì số tiền lãi tỉ lệ thuận với số vốn đã góp nên ta có:
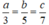
Theo tính chất của dãy tỉ số bằng nhau ta có:
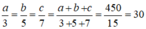
a/3 = 30 ⇒ a = 3.30 = 90
b/5 = 30 ⇒ b = 5.30 = 150
c/7 = 30 ⇒ c = 7.30 = 210
Vậy số tiền lãi được chia cho các đơn vị theo thứ tự là 90 triệu; 150 triệu và 210 triệu

gọi số tiền lãi mà mỗi đơn vị nhận được lần lượt là x,y,z
ta có :
\(\hept{\begin{cases}x+y+z=960\text{ triệu}\\\frac{x}{3}=\frac{y}{5}=\frac{z}{7}\end{cases}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}=\frac{x+y+z}{3+5+7}=\frac{960}{15}=64\)
\(\Rightarrow\hept{\begin{cases}x=3\times64=192\text{ triệu}\\y=5\times64=320\text{ triệu}\\z=7\times64=448\text{ triệu}\end{cases}}\)

Câu 1:
Gọi a,b,của là các chữ số của số có ba chữ số cần tìm . Vì mỗi chữ số a,b,của không vượt quá 9 và ba chữ số a,b,của không thể đồng thời bằng 0 , vì khi đó ta không được số có ba chữ số nên: 1 ≤ a+b+c ≤ 27
Mặt khác số phải tìm là bội của 18 nên a+b+c =9 hoặc a+b+c = 18 hoặc a+b+c=17
Theo giả thiết, ta có: \(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=\frac{a+b+c}{6}\) Do đó: ( a+b+c) chia hết cho 6
Nên : a+b+c =18 ⇒\(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=\frac{18}{6}=3\)⇒ a=3; b=6 ; của =9
Vì số phải tìm chia hết cho 18 nênchữ số hàng đơn vị của nó phải là số chẵn.
Vậy các số phải tìm là: 396; 936.

Gọi số tiền vốn lần lượt là a,b,c(đồng)
Đk:a,b,c<450
a,b,c thuộc N*
Theo bài ra, ta có:
a/3=b/5=c/7 và a+b+c=450
Theo tính chất dãy tỉ số bằng nhau, ta có:
a/3=b/5=c/7=a+b+c/3+5+7=450/15=30
Với:
a/3=30=>a=3.30=90
b/5=30=>b=5.30=150
c/7=30=>c=7.30=210

gọi số tiền vốn lần lượt là a, b, c(đồng)
đk: a, b, c<720
a, b, c thuộc N*
Theo bài ra, ta có:
a/7=b/9=c/8 và a+b+c= 720
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
a/7=b/8=c/9=a+b+c/7+8+9=720/24=30
a/7=30=>a=210
b/8=30=>b=240
c/9=30=>c=270

Bạn Click vô để tham khảo nhé:
Câu hỏi của Ho Pham Phu An - Toán lớp 7 - Học toán với OnlineMath
Bài 9:
Gọi số tiền lãi mà mỗi đơn vị được chia theo lần lượt là:
\(x;y;z\) (triệu đồng); Điều kiện: \(x;y;z\) > 0
Theo bài ra ta có: \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}\) = \(\dfrac{y}{4}\) = \(\dfrac{z}{5}\) = \(\dfrac{x+y+z}{3+4+5}\) = \(\dfrac{600}{12}\) = 50
\(x\) = 50.3 = 150
y = 50.4 = 200
z = 50.5 = 250
Kết luận: Số tiền lãi mỗi đội nhận được theo thứ tự từ ít đến nhiều lần lượt là:
150 triệu; 200 triệu; 250 triệu.
Bài 10:
Gọi độ dài các cạnh của tam giác theo thứ tự từ bé đến lớn lần lượt là:
\(x;y;z\) (cm) điều kiện \(x;y;z>0\)
Theo bài ra ta có:
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{6}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{6}=\) \(\dfrac{z-x}{6-4}\) = \(\dfrac{8}{2}\) = 4
\(x=4.4\) = 16
y = 4.5 = 20
z = 4.6 = 24
Kết luận:
Độ dài các cạnh tam giác theo thứ tự từ bé đến lớn lần lượt là:
16 cm; 20 cm; 24 cm