Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

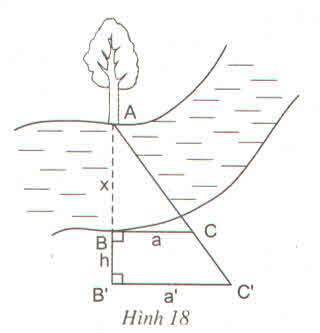
Ta có:
ABAB′ABAB′ = BCBC′BCBC′ mà AB' = x + h nên
xx+hxx+h = aa′aa′ <=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x= aha′−aaha′−a
Vậy khoảng cách AB bằng aha′−a

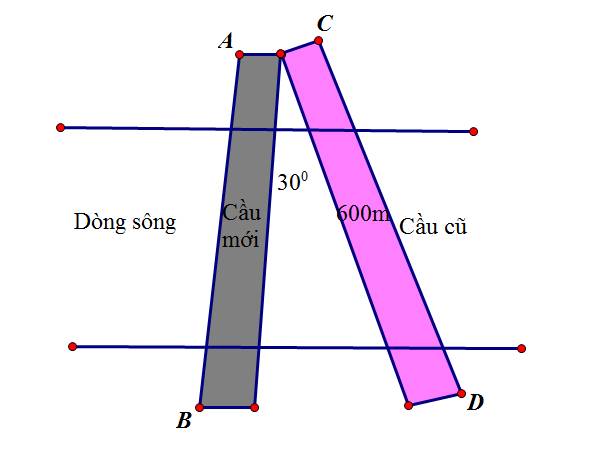
Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès, ta có:
\(\dfrac{{A{\rm{E}}}}{{AB}} = \dfrac{{CE}}{{C{\rm{D}}}}\) hay \(\dfrac{{400}}{{300}} = \dfrac{{500}}{{C{\rm{D}}}}\)
Suy ra \(C{\rm{D}} = \dfrac{{300.500}}{{400}} = 375\) (m).
Vậy khoảng cách giữa C và D bằng 375 m

mình copy ở đây : http://kenh14.vn/kham-pha/nhung-bai-toan-gay-tranh-cai-do-ban-giai-duoc-20140908094119699.chn .
bài này làm lâu lắm .
Phương án đầu tiên mà hầu hết mọi người nghĩ đến là để người đàn ông nhanh nhất đi trước và người thứ nhất sẽ lần lượt quay lại dẫn đường cho 3 người còn lại qua cầu.
Tổng cộng sẽ mất: 10 phút (D) + 1 phút (A quay lại) + 7 phút (A+C) + 1 phút (A quay lại) + 2 (A+B) = 21 phút. Nếu vậy thì bài toán quá dễ rồi.
Để giảm thời gian, chúng ta nên tìm cách cho D và C đi với nhau. Nếu họ đi qua cầu đầu tiên, họ sẽ cần một người quay lại đón người khác.
Như thế thì quá mất thời gian. Thử để A đi cùng B và để A đợi ở phía kia cây cầu. Sau khi B quay lại, C và D sẽ qua cầu và đưa đuốc cho A đón B sang.
A và B qua cầu => 2 phút
B quay lại => 2 phút
C và D qua cầu => 10 phút
A quay lại => 1 phút
A và B qua cầu => 2 phút
Tổng là: 2 + 2 + 10 + 1 + 2 = 17 phút