Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

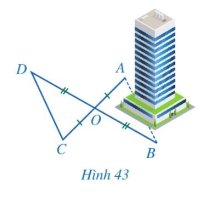
Ta có: AC giao với BD tại O.
Mà: OA = OC; OB = OD
Nên tứ giác ABCD là hình bình hành
Suy ra AB = CD = 100m.

Theo đề bài, ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và AB // EF, áp dụng định lí Thalès, ta có:
\(\dfrac{{EC}}{{BE}} = \dfrac{{CF}}{{AF}}\) hay \(\dfrac{{30}}{{BE}} = \dfrac{{20}}{{40}}\)
Suy ra \(BE = \dfrac{{30.40}}{{20}} = 60\) (m).
Vậy khoảng cách giữa hai vị trí B và E bằng 60 m.

Xét ΔCAB có FE//AB
nên \(\dfrac{CF}{FA}=\dfrac{CE}{EB}\)
=>\(\dfrac{30}{EB}=\dfrac{20}{40}=\dfrac{1}{2}\)
=>\(EB=30\cdot2=60\left(m\right)\)

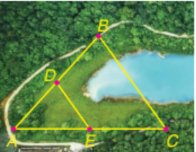
Trong tam giác ABC có D, E lần lượt là trung điểm của AB và AC nên D ∈ AB; E ∈ AC và AD = BD; AE = EC.
Suy ra DE là đường trung bình của tam giác ABC.
Do đó \(DE = \frac{1}{2}BC\) suy ra BC = 2DE = 2 . 500 = 1 000 (m)
Vậy khoảng cách giữa hai điểm B và C bằng 1 000 m.

Xét ΔCAB có FE//AB
nên FE/AB=CF/CA
=>6/AB=4/10=2/5
=>AB=15(m)

Ta có: NM//AB
=> \(\dfrac{NM}{AB}=\dfrac{CN}{AC}< =>AB=1,5\cdot\dfrac{20}{1,25}=24\left(m\right)\)
Vậy tòa nhà đó cao 24m

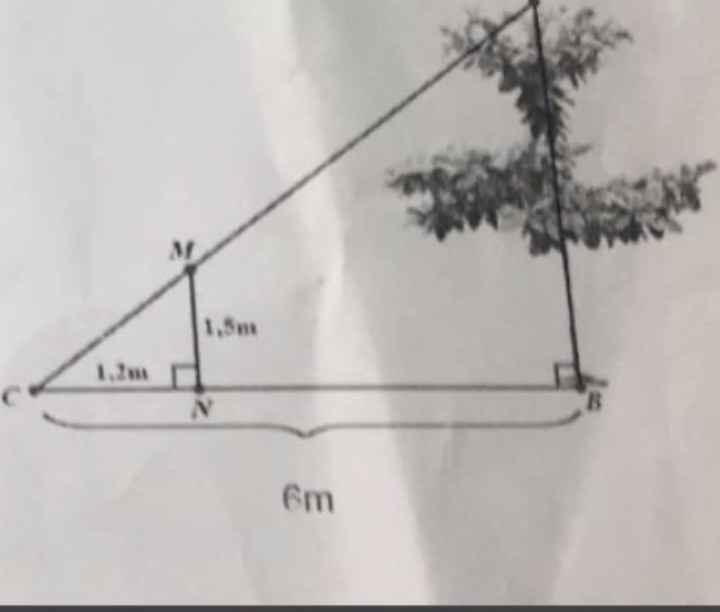
Ta có:MN\(\perp\)CB
AB\(\perp\)CB
Do đó: MN//AB
Xét ΔCAB có MN//AB
nên \(\dfrac{MN}{AB}=\dfrac{CN}{CB}\)
=>\(\dfrac{1.5}{AB}=\dfrac{1.2}{6}=\dfrac{1}{5}\)
=>AB=1,5*5=7,5(m)

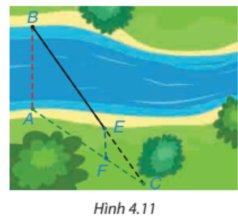
Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès, ta có:
\(\dfrac{{A{\rm{E}}}}{{AB}} = \dfrac{{CE}}{{C{\rm{D}}}}\) hay \(\dfrac{{400}}{{300}} = \dfrac{{500}}{{C{\rm{D}}}}\)
Suy ra \(C{\rm{D}} = \dfrac{{300.500}}{{400}} = 375\) (m).
Vậy khoảng cách giữa C và D bằng 375 m