Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A ∩ B = {2;7} => {2;7} ∈ B
A ∪ B = {1;2;3;4;5;7} => B = {2;3;5;7}


\(A \cap \varnothing = \varnothing\)
\(A \cup \varnothing=A\)

Giải:
4.Theo đề bài ta có:
\(A=7.a+4 \)
\(=17.b+3 \)
\(=23.c+11 (a,b,c ∈ N)\)
Nếu ta thêm 150 vào số đã cho thì ta lần lượt có:
\(A+150=7.a+4+150=7.a+7.22=7.(a+22)\)
\(=17.b+3+150=17.b+17.9=17.(b+9)\)
\(=23.c+11+150=23.c+23.7=23.(c+7) \)
\(\Rightarrow A+150⋮7;17;23\).Nhưng 7, 17 và 23 là ba số đôi một nguyên tố cùng nhau, suy ra \(A+150⋮7.17.13=2737\)
Vậy \(A+150=2737k\left(k=1;2;3;4;...\right)\)
Suy ra: \(A=2737k-150=2737k-2737+2587=2737(k-1)+2587=2737k+2587\)
Do \(2587<2737\)
\(\Rightarrow A\div2737\) dư \(2587\)

TA có
\(\frac{a}{b}-\frac{a+c}{b+c}=\frac{a\left(b+c\right)}{b\left(b+c\right)}-\frac{b\left(a+c\right)}{b\left(b+c\right)}\)
\(=\frac{ab+ac-ab-bc}{b\left(b+c\right)}=\frac{ac-bc}{b\left(b+c\right)}=\frac{c\left(a-b\right)}{b\left(b+c\right)}\)
vì a>b => a-b > 0 => c(a-b) > 0
=> \(\frac{c\left(a-b\right)}{b\left(b+c\right)}>0\)
\(=>\frac{a}{b}-\frac{a+c}{b+c}>0\)
\(=>\frac{a}{b}>\frac{a+c}{b+c}\)
=> đpcm
b) Ta có a+b < a+b+c ; b+c < a+b+c ; c+a < a+b+c
\(=>\frac{a}{a+b}>\frac{a}{a+b+c};\frac{b}{b+c}>\frac{b}{a+b+c};\frac{c}{c+a}>\frac{c}{a+b+c}\)
\(=>\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}>\frac{a+b+c}{a+b+c}=1\) (1)
Lại có
Áp dùng câu a ta có a< a+b ; b< b+c ; c<c+a
=> \(\frac{a}{a+b}< \frac{a+c}{a+b+c};\frac{b}{b+c}< \frac{b+a}{a+b+c};\frac{c}{c+a}< \frac{c+b}{a+b+c}\)
\(=>\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}< \frac{2\left(a+b+c\right)}{a+b+c}=2\) (2)
Từ (1) và (2) => dpcm

Bài 1 :
\(a)\)Ta có :
\(13< 4x\le21\)
\(\Leftrightarrow\)\(\frac{13}{4}< \frac{4x}{4}< \frac{21}{4}\)
\(\Leftrightarrow\)\(3,25< x< 5,25\)
\(\Rightarrow\)\(x=5\)
\(\Rightarrow\)\(A=\left\{5\right\}\)
Các tập hợp con của tập hợp \(A\) : \(B=\left\{\varnothing\right\}\)\(;\)\(C=\left\{5\right\}\)
\(b)\) Ta có : \(x=ab\)
\(\Rightarrow\)\(x=3.2=6\)
Hoặc \(x=3.6=18\)
Hoặc \(x=9.2=18\)
Hoặc \(x=9.6=54\)
Vậy \(C=\left\{6;18;54\right\}\)
Chúc bạn học tốt ~
Bài 5 :
Ta có :
\(\overline{2x3y}\) chia hết cho 2 và 5 \(\Rightarrow\)\(y=0\)
Lại có : \(\overline{2x3y}\) chia 9 dư 1 \(\Rightarrow\)\(2+x+3+y-1⋮9\)
\(\Leftrightarrow\)\(2+x+3+0-1⋮9\)
\(\Leftrightarrow\)\(x+4⋮9\)
Mà \(0\le x\le9\) nên \(x=5\)
Vậy \(x=5\) và \(y=0\)
Chúc bạn học tốt ~
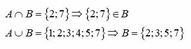
\(A=\left\{1;2;4;7\right\}\)
mà \(A\cup B=\left\{1;2;3;4;5;7\right\}\)
\(A\cap B=\left\{2;7\right\}\) \(\)
\(\Rightarrow B=\left\{2;7;3;5\right\}\)