


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



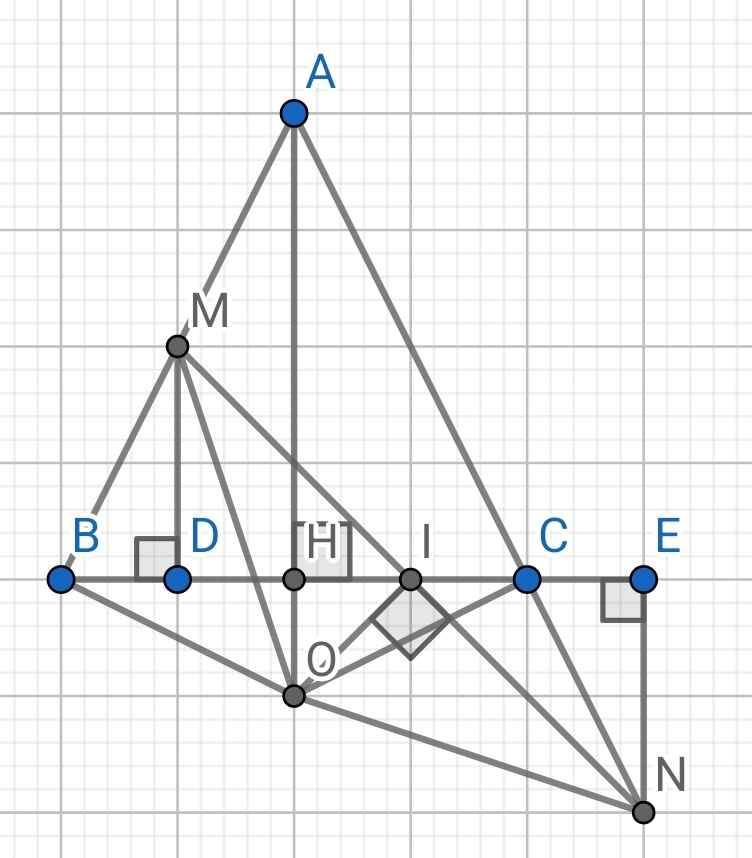 a) ∆ABC cân tại A
a) ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
Mà ∠ACB = ∠ECN (đối đỉnh)
⇒ ∠ABC = ∠ECN
⇒ ∠DBM = ∠ECN
Xét hai tam giác vuông: ∆DBM và ∆ECN có:
BD = CE (gt)
∠DBM = ∠ECN (cmt)
⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)
⇒ DM = EN (hai cạnh tương ứng)
b) Do DM ⊥ BC (gt)
EN ⊥ BC (gt)
⇒ DM // EN
⇒ ∠DMI = ∠ENI (so le trong)
Xét hai tam giác vuông: ∆DMI và ∆ENI có:
DM = EN (cmt)
∠DMI = ∠ENI (cmt)
⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)
⇒ MI = NI (hai cạnh tương ứng)
⇒ I là trung điểm của MN
⇒ BC cắt MN tại trung điểm I của MN
c) Do AH ⊥ BC nên AH là đường cao của ∆ABC
Mà ∆ABC cân tại A
AH cũng là đường phân giác của ∆ABC
⇒ ∠BAH = ∠CAH
⇒ ∠BAO = ∠CAO
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆OAB và ∆OAC có:
OA là cạnh chung
∠BAO = ∠CAO (cmt)
AB = AC (cmt)
⇒ ∆OAB = ∆OAC (c-g-c)
⇒ OB = OC (hai cạnh tương ứng)
Ta có:
I là trung điểm MN (cmt)
OI ⊥ MN (gt)
⇒ OI là đường trung trực của MN
⇒ OM = ON
Do ∆DBM = ∆ECN (cmt)
⇒ BM = CN (hai cạnh tương ứng)
Xét ∆OBM và ∆OCN có:
OB = OC (cmt)
OM = ON (cmt)
BM = CN (cmt)
⇒ ∆OBM = ∆OCN (c-c-c)
d) Do ∆OBM = ∆OCN (cmt)
⇒ ∠OBM = ∠OCN (hai góc tương ứng)
Do ∆OAB = ∆OAC (cmt)
⇒ ∠OBA = ∠OCA (hai góc tương ứng)
⇒ ∠OBM = ∠OCA
Mà ∠OBM = ∠OCN (cmt)
⇒ ∠OCN = ∠OCA
Mà ∠OCN + ∠OCA = 180⁰ (kề bù)
⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AC
a) ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
Mà ∠ACB = ∠ECN (đối đỉnh)
⇒ ∠ABC = ∠ECN
⇒ ∠DBM = ∠ECN
Xét hai tam giác vuông: ∆DBM và ∆ECN có:
BD = CE (gt)
∠DBM = ∠ECN (cmt)
⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)
⇒ DM = EN (hai cạnh tương ứng)
b) Do DM ⊥ BC (gt)
EN ⊥ BC (gt)
⇒ DM // EN
⇒ ∠DMI = ∠ENI (so le trong)
Xét hai tam giác vuông: ∆DMI và ∆ENI có:
DM = EN (cmt)
∠DMI = ∠ENI (cmt)
⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)
⇒ MI = NI (hai cạnh tương ứng)
⇒ I là trung điểm của MN
⇒ BC cắt MN tại trung điểm I của MN
c) Do AH ⊥ BC nên AH là đường cao của ∆ABC
Mà ∆ABC cân tại A
AH cũng là đường phân giác của ∆ABC
⇒ ∠BAH = ∠CAH
⇒ ∠BAO = ∠CAO
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆OAB và ∆OAC có:
OA là cạnh chung
∠BAO = ∠CAO (cmt)
AB = AC (cmt)
⇒ ∆OAB = ∆OAC (c-g-c)
⇒ OB = OC (hai cạnh tương ứng)
Ta có:
I là trung điểm MN (cmt)
OI ⊥ MN (gt)
⇒ OI là đường trung trực của MN
⇒ OM = ON
Do ∆DBM = ∆ECN (cmt)
⇒ BM = CN (hai cạnh tương ứng)
Xét ∆OBM và ∆OCN có:
OB = OC (cmt)
OM = ON (cmt)
BM = CN (cmt)
⇒ ∆OBM = ∆OCN (c-c-c)
d) Do ∆OBM = ∆OCN (cmt)
⇒ ∠OBM = ∠OCN (hai góc tương ứng)
Do ∆OAB = ∆OAC (cmt)
⇒ ∠OBA = ∠OCA (hai góc tương ứng)
⇒ ∠OBM = ∠OCA
Mà ∠OBM = ∠OCN (cmt)
⇒ ∠OCN = ∠OCA
Mà ∠OCN + ∠OCA = 180⁰ (kề bù)
⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AC

 a) ∆ABC cân tại A
a) ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
Mà ∠ACB = ∠ECN (đối đỉnh)
⇒ ∠ABC = ∠ECN
⇒ ∠DBM = ∠ECN
Xét hai tam giác vuông: ∆DBM và ∆ECN có:
BD = CE (gt)
∠DBM = ∠ECN (cmt)
⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)
⇒ DM = EN (hai cạnh tương ứng)
b) Do DM ⊥ BC (gt)
EN ⊥ BC (gt)
⇒ DM // EN
⇒ ∠DMI = ∠ENI (so le trong)
Xét hai tam giác vuông: ∆DMI và ∆ENI có:
DM = EN (cmt)
∠DMI = ∠ENI (cmt)
⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)
⇒ MI = NI (hai cạnh tương ứng)
⇒ I là trung điểm của MN
⇒ BC cắt MN tại trung điểm I của MN
c) Do AH ⊥ BC nên AH là đường cao của ∆ABC
Mà ∆ABC cân tại A
AH cũng là đường phân giác của ∆ABC
⇒ ∠BAH = ∠CAH
⇒ ∠BAO = ∠CAO
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆OAB và ∆OAC có:
OA là cạnh chung
∠BAO = ∠CAO (cmt)
AB = AC (cmt)
⇒ ∆OAB = ∆OAC (c-g-c)
⇒ OB = OC (hai cạnh tương ứng)
Ta có:
I là trung điểm MN (cmt)
OI ⊥ MN (gt)
⇒ OI là đường trung trực của MN
⇒ OM = ON
Do ∆DBM = ∆ECN (cmt)
⇒ BM = CN (hai cạnh tương ứng)
Xét ∆OBM và ∆OCN có:
OB = OC (cmt)
OM = ON (cmt)
BM = CN (cmt)
⇒ ∆OBM = ∆OCN (c-c-c)
d) Do ∆OBM = ∆OCN (cmt)
⇒ ∠OBM = ∠OCN (hai góc tương ứng)
Do ∆OAB = ∆OAC (cmt)
⇒ ∠OBA = ∠OCA (hai góc tương ứng)
⇒ ∠OBM = ∠OCA
Mà ∠OBM = ∠OCN (cmt)
⇒ ∠OCN = ∠OCA
Mà ∠OCN + ∠OCA = 180⁰ (kề bù)
⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AC

Lời giải:
Trên $AC$ lấy $E$ sao cho $AB=AE$. Xét tam giác $ABD$ và $AED$ có:
$\widehat{BAD}=\widehat{EAD}$ (do $AD$ là tia phân giác $\widehat{A}$)
$AD$ chung
$AB=AE$
$\Rightarrow \triangle ABD=\triangle AED$ (c.g.c)
$\Rightarrow BD=DE(1)$ và $\widehat{ABD}=\widehat{AED}$
Có:
$\widehat{DEC}=180^0-\widehat{AED}=180^0-\widehat{ABD}=\widehat{ECD}+\widehat{BAC}> \widehat{ECD}$
$\Rightarrow DC> DE(2)$
Từ $(1); (2)\Rightarrow DC> DB$

\(\widehat{M_1}\) = \(\widehat{M_3}\) (hai góc đối đỉnh)
\(\widehat{M_3}\) + \(\widehat{N_1}\) = 1800 (hai góc trong cùng phía)
\(\widehat{M_3}\) = 1800 - \(\widehat{N_1}\)
\(\widehat{M_3}\) = 1800 - 500
\(\widehat{M_3}\) = 1300
⇒ \(\widehat{M_1}\) = 1300
Kết luận: \(\widehat{M_1}\) = 1300

(0,5 )2 .4= ( 0,5 . 2 )2 = 12 = 1
( 0,5)3 . 8 = ( 0,5 . 2 )3 = 13 = 1
(0,5)3 . 32 = ( 0,5 . 2 )3 .22 = 13 .22 = 1.4 = 4
( 0,5)6 . 64 = ( 0,5 . 2 )6 = 16 = 1
5, 0,252 .16 = (0,25.4)2 = 12 = 1
6,(0,25)3 .64 = (0,25 .4 )3 = 13 =1
7,(0,2)2 .25 = ( 0,2 .5 )2 = 12 = 1
8,( 0,2 )3 .125 = ( 0,2 . 5 )3 = 13 = 1

Câu b đề thiếu rồi em, cần biết quan hệ giữa a và b nữa mới tính được
Bài 4:
a; A = \(\dfrac{4a-5b}{6a+b}\); biết \(\dfrac{a}{b}\) = \(\dfrac{2}{3}\)
\(\dfrac{a}{b}\) = \(\dfrac{2}{3}\) ⇒ a = \(\dfrac{2}{3}\).b
Thay a = \(\dfrac{2}{3}\)b vào biểu thức A ta có:
A = \(\dfrac{4.\dfrac{2}{3}.b-5.b}{6.\dfrac{2}{3}.b+b}\)
A = \(\dfrac{b.\left(\dfrac{8}{3}-5\right)}{b.\left(4+1\right)}\)
A = \(\dfrac{\dfrac{-7}{3}}{5}\)
A = \(\dfrac{-7}{15}\)