Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)0,6.a
b)\(a^2\).(a-3)
c)36.(a-1)
d)\(\dfrac{1.a^2}{a-b}\).(a-b)

bạn tham khảo nha : https://loigiaihay.com/bai-76-trang-41-sgk-toan-9-tap-1-c44a26988.html

a) Ta có:
+)√25+9=√34+)25+9=34.
+)√25+√9=√52+√32=5+3+)25+9=52+32=5+3
=8=√82=√64=8=82=64.
Vì 34<6434<64 nên √34<√6434<64
Vậy √25+9<√25+√925+9<25+9
b) Với a>0,b>0a>0,b>0, ta có
+)(√a+b)2=a+b+)(a+b)2=a+b.
+)(√a+√b)2=(√a)2+2√a.√b+(√b)2+)(a+b)2=(a)2+2a.b+(b)2
=a+2√ab+b=a+2ab+b
=(a+b)+2√ab=(a+b)+2ab.
Vì a>0, b>0a>0, b>0 nên √ab>0⇔2√ab>0ab>0⇔2ab>0
⇔(a+b)+2√ab>a+b⇔(a+b)+2ab>a+b
⇔(√a+√b)2>(√a+b)2⇔(a+b)2>(a+b)2
⇔√a+√b>√a+b⇔a+b>a+b (đpcm)
a, Ta có : \(\sqrt{25+9}=\sqrt{34}\)
\(\sqrt{25}+\sqrt{9}=5+3=8=\sqrt{64}\)
mà 34 < 64 hay \(\sqrt{25+9}< \sqrt{25}+\sqrt{9}\)
b, \(\sqrt{a+b}< \sqrt{a}+\sqrt{b}\)
bình phương 2 vế ta được : \(a+b< a+2\sqrt{ab}+b\)
\(\Leftrightarrow2\sqrt{ab}>0\)vì \(a;b>0\)nên đẳng thức này luôn đúng )
Vậy ta có đpcm

Rút gọn các biểu thức sau với x≥0x≥0:
a) 2\(\sqrt{3x}\)-4\(\sqrt{3x}\)+27-3\(\sqrt{3x}\)=27-5\(\sqrt{3x}\)
b)3\(\sqrt{2x}\)-5\(\sqrt{8x}\)+7\(\sqrt{18x}\)+28
=3\(\sqrt{2x}\)-10\(\sqrt{2x}\)+21\(\sqrt{2x}\)+28
=14\(\sqrt{2x}\)+28=14(\(\sqrt{2x}\)+2)
a) \(2\sqrt{3x}-4\sqrt{3x}+27-3\sqrt{3x}\)
\(=\left(2\sqrt{3x}-4\sqrt{3x}-3\sqrt{3x}\right)+27\)
\(=-5\sqrt{3x}+27\)

a, \(\sqrt{\frac{2a}{3}}.\sqrt{\frac{3a}{8}}=\sqrt{\frac{6a^2}{24}}=\sqrt{\frac{a^2}{4}}=\left|\frac{a}{2}\right|=\frac{a}{2}\)
do \(a\ge0\)
b, \(\sqrt{13a}.\sqrt{\frac{52}{a}}=\sqrt{\frac{676a}{a}}=\sqrt{676}=26\)
c, \(\sqrt{5a}.\sqrt{45a}-3a=\sqrt{225a^2}-3a=\left|15a\right|-3a\)
\(=15a-3a=12a\)do a > 0
d, \(=\left(3-a\right)^2-\sqrt{0,2}.\sqrt{180a^2}\)
\(=\left(3-a\right)^2-\sqrt{36a^2}=\left(3-a\right)^2-\left|6a\right|\)
Với \(a\ge0\Rightarrow\left(3-a\right)^2-6a=a^2-6a+9-6a=a^2-12a+9\)
Với \(a< 0\Rightarrow\left(3-a\right)^2+6a=a^2-6a+9+6a=a^2+9\)

a, Ta có \(\sqrt{25-16}=\sqrt{9}=3\)
\(\sqrt{25}-\sqrt{16}=5-4=1\)
Do 3 > 1 nên \(\sqrt{25-16}>\sqrt{25}-\sqrt{16}\)
a) căn 25 - 16 > căn 25 - căn 16
b)Với a>b>0a>b>0 nên \sqrt{a},\sqrt{b},\sqrt{a-b}a,b,− đều xác định
Để so sánh \sqrt{a}-\sqrt{b}a−b và \sqrt{a-b}− ta quy về so sánh \sqrt{a}a và \sqrt{a-b}+\sqrt{b}−+b.
+) (\sqrt{a})^2=a(a)2=a.
+) (\sqrt{a-b}+\sqrt{b})^2=(\sqrt{a-b})^2+2\sqrt{a-b}.\sqrt{b}+(\sqrt{b})^2=a-b+b+2\sqrt{a-b}.\sqrt{b}=a+2\sqrt{a-b}.\sqrt{b}(−+b)2=(−)2+2−.b+(b)2=a−b+b+2−.b=a+2−

a) \sqrt{-9a}-\sqrt{9+12 a+4 a^{2}}−9a−9+12a+4a2
=\sqrt{-9 a}-\sqrt{3^{2}+2.3 .2 a+(2 a)^{2}}=−9a−32+2.3.2a+(2a)2
=\sqrt{3^{2} \cdot(-a)}-\sqrt{(3+2 a)^{2}}=32⋅(−a)−(3+2a)2
=3 \sqrt{-a}-|3+2 a|=3−a−∣3+2a∣
Thay a=-9a=−9 ta được:
3 \sqrt{9}-|3+2 \cdot(-9)|=3.3-15=-639−∣3+2⋅(−9)∣=3.3−15=−6.
b) Điều kiện: m \neq 2m=2

LG a
(1−a√a1−√a+√a).(1−√a1−a)2=1(1−aa1−a+a).(1−a1−a)2=1 với a≥0a≥0 và a≠1a≠1
Phương pháp giải:
+ Biến đối vế trái thành vế phải ta sẽ có điều cần chứng minh.
+ √A2=|A|A2=|A|.
+ |A|=A|A|=A nếu A≥0A≥0,
|A|=−A|A|=−A nếu A<0A<0.
+ Sử dụng các hằng đẳng thức:
a2+2ab+b2=(a+b)2a2+2ab+b2=(a+b)2
a2−b2=(a+b).(a−b)a2−b2=(a+b).(a−b).
a3−b3=(a−b)(a2+ab+b2)a3−b3=(a−b)(a2+ab+b2).
Lời giải chi tiết:
Biến đổi vế trái để được vế phải.
Ta có:
VT=(1−a√a1−√a+√a).(1−√a1−a)2VT=(1−aa1−a+a).(1−a1−a)2
=(1−(√a)31−√a+√a).(1−√a(1−√a)(1+√a))2=(1−(a)31−a+a).(1−a(1−a)(1+a))2
=((1−√a)(1+√a+(√a)2)1−√a+√a).(11+√a)2=((1−a)(1+a+(a)2)1−a+a).(11+a)2
=[(1+√a+(√a)2)+√a].1(1+√a)2=[(1+a+(a)2)+a].1(1+a)2
=[(1+2√a+(√a)2)].1(1+√a)2=[(1+2a+(a)2)].1(1+a)2
=(1+√a)2.1(1+√a)2=1=VP=(1+a)2.1(1+a)2=1=VP.
LG b
a+bb2√a2b4a2+2ab+b2=|a|a+bb2a2b4a2+2ab+b2=|a| với a+b>0a+b>0 và b≠0b≠0
Phương pháp giải:
+ Biến đối vế trái thành vế phải ta sẽ có điều cần chứng minh.
+ √A2=|A|A2=|A|.
+ |A|=A|A|=A nếu A≥0A≥0,
|A|=−A|A|=−A nếu A<0A<0.
+ Sử dụng các hằng đẳng thức:
a2+2ab+b2=(a+b)2a2+2ab+b2=(a+b)2
a2−b2=(a+b).(a−b)a2−b2=(a+b).(a−b).
a3−b3=(a−b)(a2+ab+b2)a3−b3=(a−b)(a2+ab+b2).
Lời giải chi tiết:
Ta có:
VT=a+bb2√a2b4a2+2ab+b2VT=a+bb2a2b4a2+2ab+b2
=a+bb2√(ab2)2(a+b)2=a+bb2(ab2)2(a+b)2
=a+bb2√(ab2)2√(a+b)2=a+bb2(ab2)2(a+b)2
=a+bb2|ab2||a+b|=a+bb2|ab2||a+b|
=a+bb2.|a|b2a+b=|a|=VP=a+bb2.|a|b2a+b=|a|=VP
Vì a+b>0⇒|a+b|=a+ba+b>0⇒|a+b|=a+b.


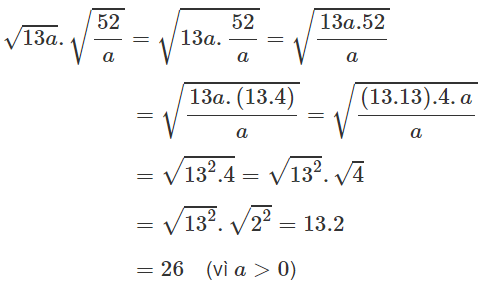

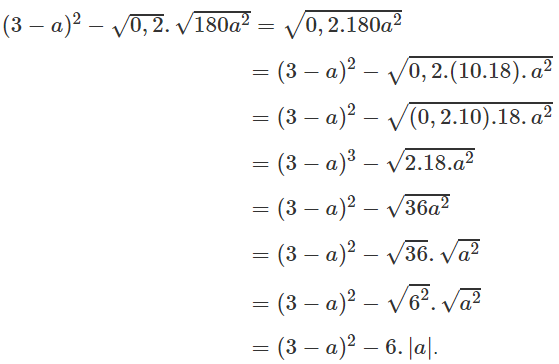
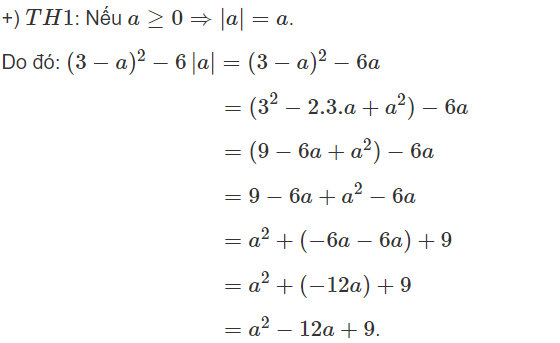
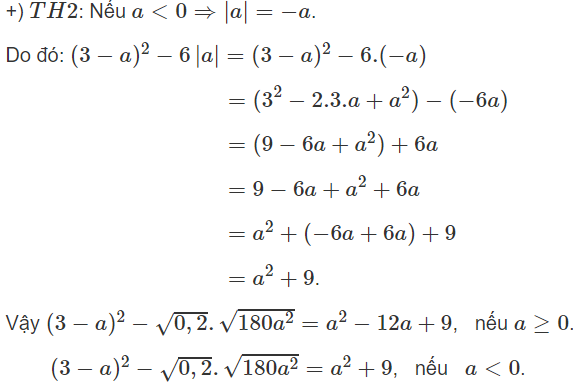
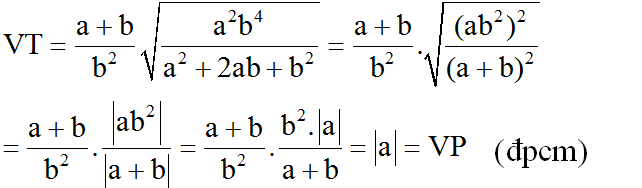
a) -√a b) -5ab√ab
) -\sqrt{a}−a; b) -5 a b \sqrt{a b}−5abab.