Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do AB // CD ( GT )
⇒^A+^C=180o
⇒2^C+^C=180o
⇒3^C=180o
⇒^C=60o
⇒ ^A = 60o * 2 = 120o
Do ABCD là hình thang cân
⇒ ^C = ^D
Mà ^C = 60o
⇒ ^D = 60o
AB // CD ⇒ ^D + ^B = 180o
⇒ˆB=180o − 60o = 120o
Vậy ^A = ^B = 120o ; ^C= ^D = 60o
Xét 2 tam giác : Tam giác ADB và tam giác BCA có :
AB : Cạnh chung
^DAB=^CBA (Tính chất của hình thang cân)
AC = BD ( Tính chất của hình thang cân)
⇒ ΔADB = ΔBCA ( c−g−c)
⇒ ^CAB = ^DBA (2 góc tương ứng)
⇒ ^OAB = ^OBA
=> Tam giác OAB cân
=> OA = OB
=> Điều phải chứng minh

a: Xét ΔABC và ΔBAD có
AB chung
BC=AD
AC=BD
=>ΔABC=ΔBAD
=>góc OBA=góc OAB
=>OA=OB
OA+OC=AC
OB+OD=BD
mà OA=OB và AC=BD
nên OC=OD
b: Xét ΔEDC có AB//DC
nên EA/AD=EB/BC
mà AD=BC
nên EA=EB
EA+AD=ED
EB+BC=EC
mà EA=EB và AD=BC
nên ED=EC
EA=EB
OA=OB
=>EO là trung trực của AB
EC=ED
OC=OD
=>EO là trung trực của CD

a ) Xét Δ∆ADC và Δ∆BCD, ta có:
AD = BC (tính chất hình thang cân)
∠∠(ADC) = ∠∠(BCD) (gt)
DC chung
Do đó: Δ∆ADC = Δ∆BCD (c.g.c) ⇒ ∠C1∠�1= ∠D1∠�1
Trong Δ∆OCD ta có: ∠C1∠�1= ∠D1∠�1 ⇒ Δ∆OCD cân tại O ⇒ OC = OD (1)
AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.
b)
ADC=ˆBCD(gt)⇒ˆODC=ˆOCD���^=���^(��)⇒���^=���^

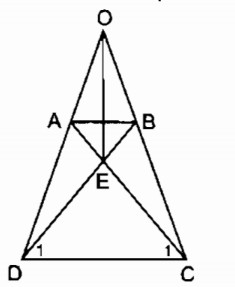
1.
O A B D C E
+) Tứ giác ABCD kà hình thang cân => góc ADC = BCD và AD = BC
=> tam giác ODC cân tại O => OD = OC
mà AD = BC => OA = OB
+) tam giác ODB và OCA có: OD = OC; góc DOC chung ; OB = OA
=> Tam giác ODB = OCA (c - g - c)
=> góc ODB = OCA mà góc ODC = OCD => góc ODC - ODB = OCD - OCA
=> góc EDC = ECD => tam giác EDC cân tại E => ED = EC (2)
Từ (1)(2) => OE là đường trung trực của CD
=> OE vuông góc CD mà CD // AB => OE vuông góc với AB
Tam giác OAB cân tại O có OE là đường cao nên đồng thời là đường trung trực
vậy OE là đường trung trực của AB

Bài làm :
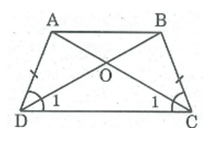
Ta có hình vẽ :
A B C D O
Xét 2 tam giác : Tam giác ADB và tam giác BCA có :
\(\hept{\begin{cases}AB-\text{Cạnh chung}\\\widehat{DAB}=\widehat{CBA}\left(\text{Tính chất của hình thang cân}\right)\\AC=BD\left(\text{Tính chất của hình thang cân}\right)\end{cases}}\)
\(\Rightarrow\Delta ADB=\Delta BCA\left(c-g-c\right)\)
\(\Rightarrow\widehat{CAB}=\widehat{DBA}\left(\text{2 góc tương ứng}\right)\)
\(\Rightarrow\widehat{OAB}=\widehat{OBA}\)
=> Tam giác OAB cân
=> OA = OB
=> Điều phải chứng minh
Xét 2 tam giác : Tam giác ADB và tam giác BCA có :
AB−Cạnh chung
^DAB=^CBA(Tính chất của hình thang cân)
AC=BD(Tính chất của hình thang cân)
⇒ΔADB=ΔBCA(c−g−c)
⇒ˆCAB=ˆDBA(2 góc tương ứng)
⇒ˆOAB=ˆOBA
=> Tam giác OAB cân
=> OA = OB
=> Điều phải chứng minh