Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Bà An gửi vào quỹ tiết kiệm: x đồng (x > 0).
Lãi suất mỗi tháng là a% tháng nên số tiền lãi sau tháng thứ nhất bằng: a%.x
Số tiền (cả gốc lẫn lãi) có được sau tháng thứ nhất: x + a%.x = (1 + a%)x
Số tiền lãi sau tháng thứ hai: (1 + a%)x.a%
Tổng số tiền lãi sau hai tháng bằng: a%.x + (1 + a%).x.a% (đồng) (1)
b) Vì sau hai tháng bà An lãi 48288 đồng với lãi suất 1,2% (tức là a = 1,2) nên thay vào (1) ta có phương trình:
1,2%.x + (1 + 1,2%).x.1,2% = 48288
⇔ 0,012x + 1,012.x.0,012 = 48288
⇔ 0,012x + 0,012144x = 48288
⇔ 0,024144.x = 48288
⇔ x = 2 000 000 (đồng).
Vậy bà An đã gửi tiết kiệm 2 000 000 đồng.

Gọi lãi suất là x (%(
Ta có sau 2 năm tổng gốc và lãi 449,44 triệu đồng.
=> \(400.\left(1+x\right)^2=449,44\\ \Leftrightarrow\left(1+x\right)^2=\dfrac{449,44}{400}=1,1236=\left(106\%\right)^2\\ \Rightarrow x\left(\%\right)=6\%\\ Vậy:x=6\)

a) Bà An gửi vào quỹ tiết kiệm: x đồng
Lãi suất là a% tháng nên số tiền lãi sau tháng thứ nhất a%.x
Số tiền có được sau tháng thứ nhất: x + a%.x = (1 + a%)x
Số tiền lãi sau tháng thứ hai: (1 + a%)x.a%
Tổng số tiền lãi sau hai tháng:
b) Vì sau hai tháng bà An lãi 48288 đồng với lãi suất 1,2% nên:
Vậy bà An đã gửi tiết kiệm 2000000 đồng.

a) Bà An gửi vào quỹ tiết kiệm: x đồng
Lãi suất là a% tháng nên số tiền lãi sau tháng thứ nhất a%.x
Số tiền có được sau tháng thứ nhất: x + a%.x = (1 + a%)x
Số tiền lãi sau tháng thứ hai: (1 + a%)x.a%
Tổng số tiền lãi sau hai tháng:
b) Vì sau hai tháng bà An lãi 48288 đồng với lãi suất 1,2% nên:
Vậy bà An đã gửi tiết kiệm 2000000 đồng.

a) Bà An gửi vào quỹ tiết kiệm: x đồng
Lãi suất là a% tháng nên số tiền lãi sau tháng thứ nhất a%.x
Số tiền lãi có được sau tháng thứ hai:
Tổng số tiền lãi sau hai tháng:
a%x+(1+a%)x.a%=(2+a%).a%xa%x+(1+a%)x.a%=(2+a%).a%x
b) Vì sau hai tháng bà An lãi 48288 đồng với lãi suất 1,2% nên:
(2+1,2%)1,2%x=48288⇔x=482882,012.0,012(2+1,2%)1,2%x=48288⇔x=482882,012.0,012
⇔x=2000000x=2000000
Vậy bà An đã gửi tiết kiệm 2000 000 đồng.
a) Bà An gửi vào quỹ tiết kiệm: x đồng ( x > 0 )
Lãi suất mỗi tháng là a% tháng nên số tiền lãi sau tháng thứ nhất bằng: a% . x
Số tiền ( cả gốc lẫn lãi ) có được sau tháng thứ nhất: x + a% . x = ( 1 + a% ) x
Số tiền lãi sau tháng thứ hai: ( 1 + a% ) x . a%
Tổng số tiền lãi sau hai tháng bằng: a% . x + ( 1 + a% ) . x . a% ( đồng ) (1)
b) Vì sau hai tháng bà An lãi 48288 đồng với lãi suất 1,2% ( tức là a = 1,2 ) nên thay vào (1) ta có phương trình:
1,2% . x + ( 1 + 1,2% ) . x .1,2% = 48288
<=> 0,012x + 1,012.x.0,012 = 48288
<=> 0,012x + 0,012144x = 48288
<=> 0,024144.x = 48288
<=> x = 2 000 000 (đồng).
Vậy bà An đã gửi tiết kiệm 2 000 000 đồng.

Gọi a là số tháng gửi với lãi suất 0,7% tháng, x là số tháng gửi với lãi suất 0,9% tháng, thì số tháng gửi tiết kiệm là: a + 6 + x. Khi đó, số tiền gửi cả vốn lẫn lãi là:
Quy trình bấm phím:
5000000 ´ 1.007 ^ ALPHA A ´ 1.0115 ^ 6 ´ 1.009 ^ ALPHA X - 5747478.359 ALPHA = 0
SHIFT SOLVE Nhập giá trị của A là 1 = Nhập giá trị đầu cho X là 1 = SHIFT SOLVE Cho kết quả X là số không nguyên.
Lặp lại quy trình với A nhập vào lần lượt là 2, 3, 4, 5, ...đến khi nhận được giá trị nguyên của X = 4 khi A = 5.
Vậy số tháng bạn Châu gửi tiết kiệm là: 5 + 6 + 4 = 15 tháng
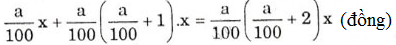
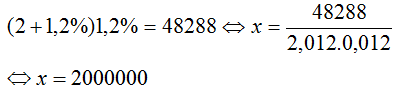
Gọi số tiền bác An gửi là x
Sau 1 tháng bác An có được x*1,072(đồng)
Sau 2 tháng bác An có được x*1,072*1,072=x*1,072^2(đồng)
Theo đề, ta có:
x*1,072^2=151805400
=>x=132098428,1(đồng)