Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Thay x=1 vào đa thức F(x) ta được:
F(1) = 14+2.13-2.12-6.1+5 = 0
=> x=1 là nghiệm của đa thức F(x)
Tương tự ta thế -1; 2; -2 vào đa thức F(x)
Vậy x=1 là nghiệm của đa thức F(x)

Đặt P(x)=0
\(\Leftrightarrow x\left(x^4+7x^3-9x^2-2x-\dfrac{1}{4}\right)=0\)
=>x=0
Đặt Q(x)=0
\(\Leftrightarrow-5x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}=0\)
hay \(x\in\varnothing\)

Lời giải:
a)
$M(x)=(x^5+5x^5)-2x^4-4x^3+3x$
$=6x^5-2x^4-4x^3+3x$
$N(x)=-6x^5+(7x^4-5x^4)+(x^3+3x^3)+4x^2-3x-1$
$=-6x^5+2x^4+4x^3+4x^2-3x-1$
b)
$M(-1)=6(-1)^5-2(-1)^4-4(-1)^3+3(-1)=-7$
$N(-2)=-6(-2)^5+2(-2)^4+4(-2)^3+4(-2)^2-3(-2)-1$
$=213$
c)
$M(x)+N(x)=(6x^5-2x^4-4x^3+3x)+(-6x^5+2x^4+4x^3+4x^2-3x-1)$
$=4x^2-1$
$M(x)-N(x)=(6x^5-2x^4-4x^3+3x)-(-6x^5+2x^4+4x^3+4x^2-3x-1)$
$=12x^5-4x^4-8x^3-4x^2+6x+1$
d)
$F(x)=M(x)+N(x)=4x^2-1=0\Leftrightarrow x^2=\frac{1}{4}$
$\Leftrightarrow x=\pm \frac{1}{2}$
Vậy $x=\pm \frac{1}{2}$ là nghiệm của $F(x)$

a: \(\Leftrightarrow-3\left(x-2\right)+\dfrac{2}{5}\cdot5\left(x-2\right)=0\)
=>-(x-2)=0
=>x=2
b: =>x2(x2-5)=0
hay \(x\in\left\{0;\sqrt{5};-\sqrt{5}\right\}\)
c: =>(x-1)(x-8)=0
=>x=1 hoặc x=8

bài 1
a) \(-\frac{1}{3}xy\).(3\(x^2yz^2\))
=\(\left(-\frac{1}{3}.3\right)\).\(\left(x.x^2\right)\).(y.y).\(z^2\)
=\(-x^3\).\(y^2z^2\)
b)-54\(y^2\).b.x
=(-54.b).\(y^2x\)
=-54b\(y^2x\)
c) -2.\(x^2y.\left(\frac{1}{2}\right)^2.x.\left(y^2.x\right)^3\)
=\(-2x^2y.\frac{1}{4}.x.y^6.x^3\)
=\(\left(-2.\frac{1}{4}\right).\left(x^2.x.x^3\right).\left(y.y^2\right)\)
=\(\frac{-1}{2}x^6y^3\)
Bài 3:
a) \(f\left(x\right)=-15x^2+5x^4-4x^2+8x^2-9x^3-x^4+15-7x^3\)
\(f\left(x\right)=\left(5x^4-x^4\right)-\left(9x^3+7x^3\right)-\left(15x^2+4x^2-8x^2\right)+15\)
\(f\left(x\right)=4x^4-16x^3-11x^2+15\)
b)
\(f\left(x\right)=4x^4-16x^3-11x^2+15\)
\(f\left(1\right)=4\cdot1^4-16\cdot1^3-11\cdot1^2+15\)
\(f\left(1\right)=4\cdot1^4-16\cdot1^3-11\cdot1^2+15\)
\(f\left(1\right)=-8\)
\(f\left(x\right)=4x^4-16x^3-11x^2+15\)
\(f\left(-1\right)=4\cdot\left(-1\right)^4-16\cdot\left(-1\right)^3-11\cdot\left(-1\right)^2+15\)
\(f\left(-1\right)=24\)

sắp xếp:
C= \(x^5\) + 3\(x^4\) - 2\(x^3\) - 9\(x^2\) + 11x - 6
B= \(x^5\) + \(3x^4\) - \(2x^3\) - \(10x^2\) +9x + 4
B= \(x^5\) + \(3x^4\) - \(2x^3\) - \(10x^2\) +9x + 4
+
- C= \(x^5\) - 3\(x^4\) + 2\(x^3\) + 9\(x^2\) - 11x + 6
M = \(2x^5\) - \(x^2\) - 2x + 10
Ta có M = B - C
\(\Rightarrow M=[3x^4+x^5-2\left(x^3+4\right)-10x^2+9x]\\ \\ -\left(x^5-2x^3+3x^4-9x^2+11x-6\right)\)
\(\Rightarrow M=3x^4+x^5-2x^3+4-10x^2+9x\\ -x^5+2x^3-3x^4+9x^2-11x+6\)
\(\Rightarrow M=\left(3x^4-3x^4\right)+\left(x^5-x^5\right)+\left(-2x^3+2x^3\right)\\ +\left(4+6\right)+\left(-10x^2+9x^2\right)+\left(9x-11x\right)\)
\(\Rightarrow M=10-x^2-2x\)
Vậy \(M=10-x^2-2x\)
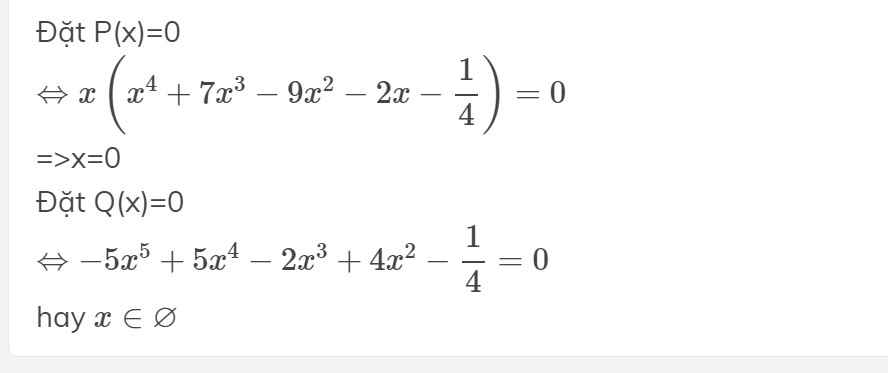
a: \(P\left(x\right)=x^5+2x^4-9x^3-x\)
\(Q\left(x\right)=5x^4+9x^3+4x^2-14\)
c:: \(M\left(x\right)=P\left(x\right)+Q\left(x\right)=x^5+7x^4+4x^2-x-14\)
d: \(M\left(2\right)=32+7\cdot16+4\cdot4-2-14=144\)
\(M\left(-2\right)=-32+7\cdot16+4\cdot4+2-14=84\)