Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔADM và ΔCBN có
\(\widehat{ADM}=\widehat{CBN}\)
AD=CB
\(\widehat{A}=\widehat{C}\)
Do đó: ΔADM=ΔCBN
Suy ra: AM=CN

a: Xét ΔADM và ΔCBN có
\(\widehat{ADM}=\widehat{CBN}\)
AD=CB
\(\widehat{A}=\widehat{C}\)
Do đó: ΔADM=ΔCBN
Suy ra: AM=CN

a: Xét ΔADM và ΔCBN có
\(\widehat{ADM}=\widehat{CBN}\)
AD=CB
\(\widehat{A}=\widehat{C}\)
Do đó: ΔADM=ΔCBN
Suy ra: AM=CN
phần c em để chữ đậm đó ạ chứ phần a em làm cách khác rồi, em cảm ơn ạ

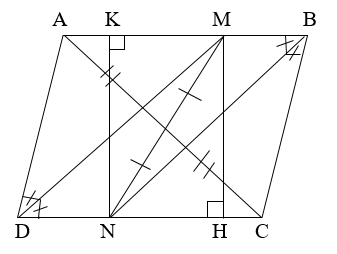
Bạn tự vẽ hình nhá!!!!
a) ABCD là hình bình hành=>góc ADC=góc ABC => góc MBN=góc MDN
Mà: góc MBN= góc BNC( so le trong) => góc BNC=góc MDN => DM//BN
b) Từ phần a ta có:
Xét DMNB có DM//BN
BM//DN (do AB//CD)
=> DMNB là hbh
c) Ta có:
góc AMD= góc MDC(so le trong) => góc ADM= góc AMD=> Tam giác AMD cân tại A
Mà: AH là đường phân giác=> AH là đường cao<=> AH vuông góc với DM (1)
=>AG vuông góc với BN ( do DM//BN) (2)
Tương tự, ta cũng chứng minh được tam giác BNC cân tại C
Mà: CF là đường PG=> CF vuông góc với BN (3)
Từ (1); (2); (3) => HEFG là hcn do có 3 góc vuông