Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Ta có ∆ABE = ∆ADF(g.c.g) => AE = AF
b, Ta có: ∆AKF ~ ∆CAF ( F ^ chung và F A K ^ = F C A ^ = 45 0 )
=> A F H F = C F A F => A F 2 = K F . C F
c, S A E F = 93 2 c m 2
d, Ta có: AE.AJ=AF.AJ=AD.FJ
=> A E . A J F J = AD không đổi

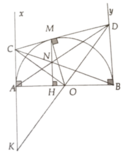
a, Kẻ OM ⊥ CD
Gọi K = OD ∩ d => ∆COK = ∆COD
=> OK = OD => OM = OA = R => CD là tiếp tuyến
b, AC+BD=CM+DM=CD ≥ AB
Do đó min (AC+BD)=AB
<=> CD//AB => ABCD là hình chữ nhật <=> AC = AO
c, AC.BD = MC.MD = O M 2 = 4 a 2
=> 1 O C 2 + 1 O D 2 = 1 4 a 2
d, Từ tính chất hai giao tuyến => MN//BD => MNAB hay MHAB;
AC//BD; MN//BD; NH//BD
=> M N B D = N H B D => MN = NH

a, Ta có: E C A ^ + O C A ^ = 90 0 và A C H ^ + O A C ^ = 90 0
mà O A C ^ = O C A ^ (do tam giác AOC cân tại O)
Suy ra E C A ^ = A C H ^
Khi đó E A C ^ = H A C ^ (cùng lần lượt phụ với E C A ^ và A C H ^ ), ta có đpcm
b, Chứng minh tương tự suy ra BC là phân giác của F B H ^
Từ đó, chứng minh được BC vuông góc HF (1)
Tam giác ABC có trung tuyến OC = 1 2 AB. Suy ra tam giác ABC vuông tại C , tức là BC vuông góc với AC (2)
Từ (1),(2) suy ra đpcm
c, Ta có : AE+BF =2OC=2R không đổi
d, Ta có A E . B F ≤ A E + B F 2 4 = R 2
suy ra AE.BF lớn nhất = R 2 óAE=BF=R
Điều này xẩy ra khi C là điểm chính giữa cung AB

a, bc^2 = ab^2 +ac^2
<=.> (ae+eb)^2 +(af+fc)^2
<=.>AE^2 +2 AE.EB +EB^2 +AF^2+FC^2+2AF,FC
<=> EF^2 +EB^2 +CF^2 +2.(EH^2+FH^2)
<=>EB^2 +CF^2 + AH ^2 + 2 AH^2 vì tứ giác EHAF là hcn suy ra AH =EF
<=>EB^2 +CF^2+3 AH^2 (đpcm)
b, cb =2a là thế nào vậy