Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cạnh của đáy thùng là :
20 : 4 = 5 (dm)
Diện tích đáy thùng là :
5 x 5 = 25 (dm2)
Ta có : 150 lít = 150 dm3
Chiều cao của dầu trong thùng là :
150 : 25 = 6 (dm)
Đáp số 6 dm.

Gọi số quýt ban đầu ở mỗi rổ là x (quả)
Muốn lấy 30 quả ở rổ thứ nhất đưa sang rổ thứ hai thì số quả ở mỗi rổ lúc đầu phải nhiều hơn 30 quả hay x > 30.
Khi đó rổ thứ nhất còn x – 30 quả; rổ thứ hai có x + 30 quả.
Vì số quả ở rổ thứ hai bằng 1/3 bình phương số quả còn lại ở rổ thứ nhất nên ta có phương trình:
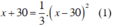
Giải phương trình (1):
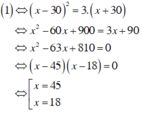
Vì x > 30 nên x = 45 thỏa mãn.
Vậy ban đầu mỗi rổ có 45 quả cam.

Hiệu hai kho là:
70,8 - 48,6 =22,2
Hiệu số phần là
5-2=3
Giá trị 1 phần là ;
22,2 : 3 = 7,4
Kho thứ hai sau khi lấy là
7,4 x 2 = 14,8
Kho thứ nhất sau khi lấy là
7,4 nhân 5 =37
Số tấn gạo lấy đi ở kho thứ hai là
48,6 - 14,8 =33.8
Vậy kho thứ 1 cũng sẽ bị lấy ra 33.8 tấn gạo
Đáp số ; 33.8

Tham khảo:
a) Gọi x là số thùng thuốc trừ sâu loại A, y là số thùng thuốc trừ sâu loại B mà nhà máy sản xuất mỗi ngày. Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- sản lượng \(C{O_2}\) tối đa là 75 kg nên \(0,25x + 0,5y \le 75\)
- sản lượng \(S{O_2}\) tối đa là 90 kg nên \(0,6x + 0,2y \le 90\)
Từ đó ta có hệ bất phương trình:
\(\left\{ \begin{array}{l}0,25x + 0,5y \le 75\\0,6x + 0,2y \le 90\\x \ge 0\\y \ge 0\end{array} \right.\)
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy, ta được như hình dưới.
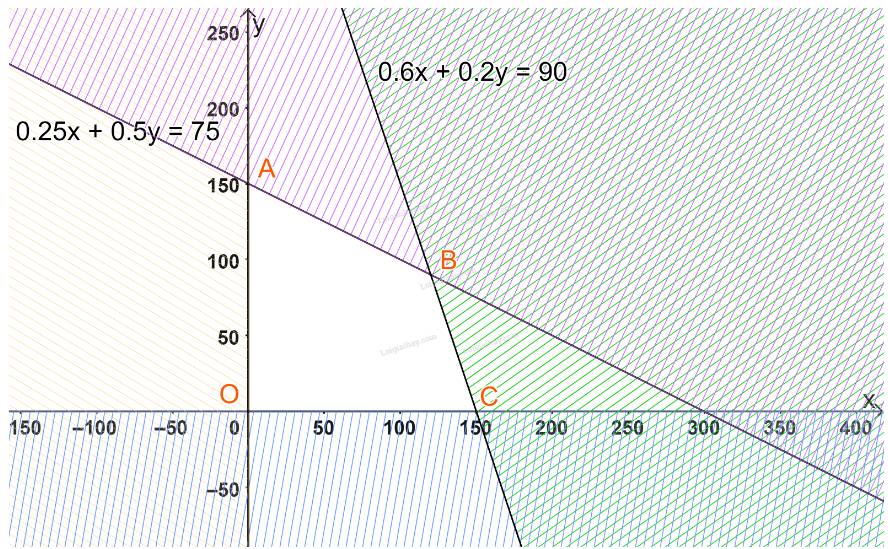
Miền không gạch chéo (miền tứ giác OABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình.
b) Nhà máy sản xuất 100 thùng loại A và 80 thùng loại B mỗi ngày tức là \(x = 100,y = 80.\)
Vì \(\left\{ \begin{array}{l}0,25.100 + 0,5.80 = 65 \le 75\\0,6.100 + 0,2.80 = 76 \le 90\\100 \ge 0\\80 \ge 0\end{array} \right.\) nên cặp số (100; 80) là một nghiệm của hệ bất phương trình a).
Do đó việc nhà máy sản xuất 100 thùng loại A và 80 thùng loại B mỗi ngày là phù hợp với quy định.
c) Vì \(0,25.60 + 0,5.160 = 95 > 75\)nên việc sản xuất 60 thùng loại A và 160 thùng loại B mỗi ngày vượt quá sản lượng \(C{O_2}\) tối đa.
Vậy việc nhà máy sản xuất 60 thùng loại A và 160 thùng loại B mỗi ngày là không phù hợp với quy định.
Sau khi lấy ở thùng 1 ra 5 lít và ở thùng 2 ra 3 lít thì số dầu còn lại ở 2 thùng là:
\(88-3-5=80\left(l\right)\)
Tổng số phần bằng nhau:
\(1+3=4\)
Khi đó, số lít dầu ở thùng 1 là:
\(80\div4\times3=60\left(l\right)\)
Số lít dầu ở thùng 1 lúc đầu là:
\(60+5=65\left(l\right)\)
Số lít dầu ở thùng 2 lúc đầu là:
\(88-65=23\left(l\right)\)
Chúc bạn học tốt
Sau khi lấy ở thùng 1 ra 5 lít và ở thùng 2 ra 3 lít thì số dầu còn lại ở 2 thùng là:
\(88-5-3=80\) (l)
Tổng số phần bằng nhau:
\(1+3=4\)
Số lít dầu ở thùng 1 là:
\(80\div4\times3+5=65\) (l)
Số lít dầu ở thùng 2 là:
\(88-65=23\) (l)
Chúc bạn học tốt