Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{15}=\dfrac{b}{16}=\dfrac{c}{14}=\dfrac{a+b+c}{15+16+14}=\dfrac{45}{45}=1\)
Do đó: a=15; b=16; c=14

Gọi `3` lớp `7A;7B;7C` thu nhặt giấy vụn lần lượt là `a,b,c` \(\left(a,b,c\in N\right)\)
Theo đề ra ta có : `a/40=b/42=c/45` và `a+b+c=254`
ADTC dãy tỉ số bằng nhau ta có :
`a/40=b/42=c/45 =(a+b+c)/(40+42+45)= 254/127=2`
`=>a/40=2=>a=2.40=80`
`=>b/42=2=>b=2.42=84`
`=>c/45=2=>c=2.45=90`
vậy ...
Gọi khối lượng giấy vụn lớp 7A,7B,7C thu được lần lượt là a,b,c
Theo đề, ta có: a/40=b/42=c/45 và a+b+c=254
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{40}=\dfrac{b}{42}=\dfrac{c}{45}=\dfrac{a+b+c}{40+42+45}=2\)
=>a=80; b=84; c=90

Gọi số giấy vụn của lớp 7A, 7B, 7C lần lượt là a; b; c
Theo đề bài, ta có:
\(\Rightarrow\frac{a}{40}+\frac{b}{42}+\frac{c}{45}\) và a + b + c = 254
Áp dụng tính chất của dãy tỉ số = nhau, ta có:
\(\frac{a}{40}=\frac{b}{42}=\frac{c}{45}=\frac{a+b+c}{40+42+45}=\frac{254}{127}=2\)
=> a = 40 . 2 = 80 (kg)
b = 42 . 2 = 84 (kg)
c = 45 . 2 = 90 (kg)
Vậy số giấy của 3 chi đội lần lượt là: 80 kg; 84 kg; 90 kg

Mốt là số cân nặng của một học sinh có tần số lớn nhất
Số học sinh cân nặng 31 kg và 32 kg là nhiều nhất với tần số là 12.
Vậy mốt là 31 và 32
Chọn đáp án D.

Mốt là số cân nặng của một học sinh có tần số lớn nhất
Số học sinh cân nặng 31 kg và 32 kg là nhiều nhất với tần số là 12.
Vậy mốt là 31 và 32
Chọn đáp án D.

Số trung bình cộng là:
X = 28 . 5 + 30 . 6 + 31 . 12 + 32 . 12 + 36 . 4 + 40 . 4 + 45 . 2 45 ≈ 32 , 7 k g
Chọn đáp án B.

| Cân nặng | 28 | 30 | 31 | 32 | 36 | y | z | 45 | x |
| Tần số | 3 | 2 | 3 | 6 | 2 | 1 | 1 | 1 | 1 |
Đa phần các bạn đều ở mức cân nặng từ 30-36 kg

a: \(-\dfrac{4}{7}-\dfrac{5}{13}\cdot\dfrac{-39}{25}+\dfrac{-1}{42}:\dfrac{-5}{6}\)
\(=\dfrac{-4}{7}+\dfrac{3}{5}+\dfrac{1}{35}\)
\(=\dfrac{-20}{35}+\dfrac{21}{35}+\dfrac{1}{35}\)
\(=\dfrac{2}{35}\)
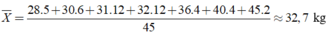
đã trả lời