Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

áp dụng định lý Pi-ta-go vào tam giác ABC vuông tại A có:
\(BC^2=AB^2+AC^2\)
\(BC^2-AB^2=AC^2\)
\(15^2-9^2=AC^2\)
\(144=AC^2\)
\(AC=12\)(cm)
b)Có BC<AC<AB
=>A<B<C
c) xét tam giác CAB và tam giác CAD có :
CA chung
DA=AB
góc CAB= gócCAD=90 độ
=>tam giác CAB=tam giác CAD(2 cạnh góc vuông)
=>CB=CD(2 cạnh tương ứng )
=>tam giác BCD cân
d) vì A là trung điểm BD=>DA=DB=>CA là đường trung tuyến DB (1)
có K là trung điểm cạnh BC=>KB=KC=\(\frac{1}{2}\)BC=\(\frac{15}{2}\)=7,5 (cm) (2)
Từ (1) và(2)=>CA =CK=7,5(cm)(trong 1 tam giác vuông đường trung tuyến bằng 1 nửa cạnh huyền)
Từ (1) =>CM=\(\frac{2}{3}\)CA
=>CM=\(\frac{2}{3}\times7,5\)
=>CM=5(cm)

Tham khảo:
a) Vì tam giác ABC vuông tại A nên \(\widehat{A}=90^0; \widehat{B}+\widehat{C}=90^0\)
Vì \(\widehat B > {45^o} \Rightarrow \widehat C < {45^o} \Rightarrow \widehat A > \widehat B > \widehat C \Rightarrow BC > AC > AB\)
b) Vì \(\widehat {BKC}\) là góc ngoài tại đỉnh K của tam giác ABK nên \(\widehat {BKC}>(\widehat {BAK}=90^0\)
Xét tam giác BCK, ta có :
\(\widehat {BKC} > {90^o} > \widehat {BCK}\)
\( \Rightarrow BC > BK\) ( quan hệ giữa góc và cạnh đối diện trong tam giác)

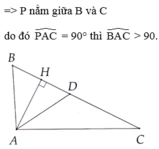
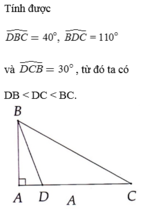
tóm tắt luôn : cạnh BD ngắn hơn các cạnh AB và AD vì nó nằm trên cạnh BC nên sẽ bị giảm độ dài