Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng


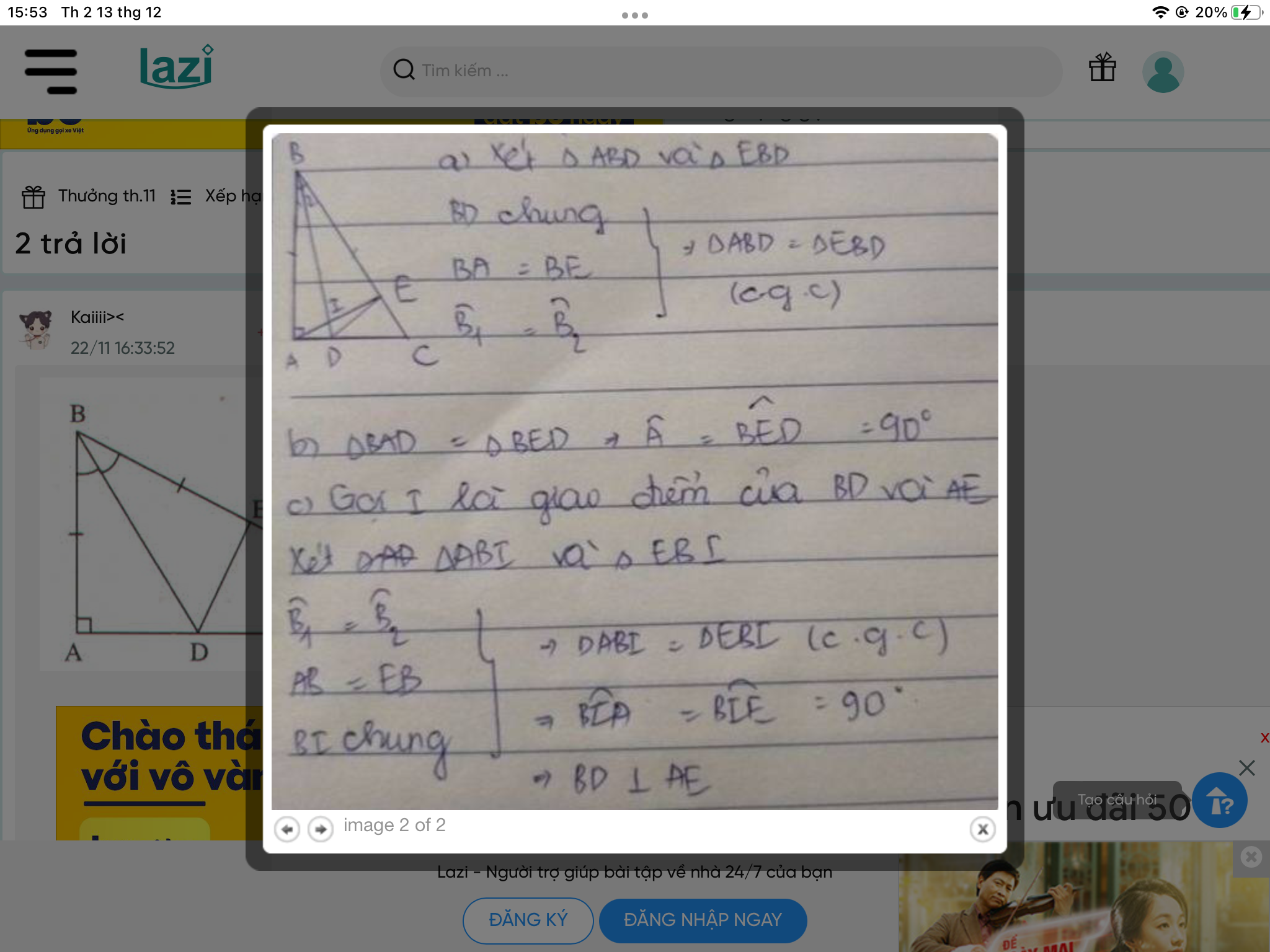
a) Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E
có: BD là cạnh chung
góc ABD = góc EBD (gt)
\Rightarrow\Delta ABD=\Delta EBD\left(ch-gn\right)⇒ΔABD=ΔEBD(ch−gn)
b) ta có: \Delta ABD=\Delta EBD\left(pa\right)ΔABD=ΔEBD(pa)
=> AB = EB = 6 cm ( 2 cạnh tương ứng)
=> EB = 6 cm
Xét tam giác ABC vuông tại Acó: AB^2+AC^2=BC^2\left(py-ta-go\right)AB2+AC2=BC2(py−ta−go)
thay số: 6^2+8^2=BC^262+82=BC2
\Rightarrow BC^2=100⇒BC2=100
\Rightarrow BC=10cm⇒BC=10cm
mà E\in BCE∈BC
=> EB + EC = BC
thay số: 6 + EC = 10
EC = 10 - 6
=> EC = 4 cm
c) ta có: \Delta ABD=\Delta EBD\left(pa\right)ΔABD=ΔEBD(pa)
=> AD = ED ( 2 cạnh tương ứng)
AB = EB ( 2 cạnh tương ứng) (1)
Xét tam giác ADI vuông tại A và tam giác EDC vuông tại E
có: AD = ED ( chứng minh trên)
góc ADI = góc EDC ( đối đỉnh)
\Rightarrow\Delta ADI=\Delta EDC\left(cgv-gn\right)⇒ΔADI=ΔEDC(cgv−gn)
=> AI = EC ( 2 cạnh tương ứng)(2)
Từ (1);(2) => AB + AI = EB + EC
=> BI = BC
=> tam giác BIC cân tại B ( định lí tam giác cân)
d) ta có: \Delta ABD=\Delta EBD\left(pa\right)ΔABD=ΔEBD(pa)
=> AD = ED ( 2 cạnh tương ứng) (1)
Xét tam giác EDC vuông tại E
có: ED < DC ( định lí cạnh góc vuông, cạnh huyền) (2)
Từ (1);(2) => AD <DC
a: Sửa đề: ΔAHD=ΔAED
Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
AH=AE
Do đó: ΔAHD=ΔAED
=>\(\widehat{HAD}=\widehat{EAD}\)
=>\(\widehat{HAD}=\widehat{CAD}\)
=>AD là phân giác của góc HAC
b: Ta có: ΔAHD=ΔAED
=>DH=DE
Xét ΔDHK vuông tại H và ΔDEC vuông tại E có
DH=DE
\(\widehat{HDK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDHK=ΔDEC
=>DK=DC
=>ΔDKC cân tại D
c: Ta có: ΔDHK=ΔDEC
=>HK=EC
Xét ΔAKC có \(\dfrac{AH}{HK}=\dfrac{AE}{EC}\)
nên HE//KC
d: Ta có: AH+HK=AK
AE+EC=AC
mà AH=AE và HK=EC
nên AK=AC
=>A nằm trên đường trung trực của KC(1)
ta có: DK=DC
=>D nằm trên đường trung trực của KC(2)
Ta có: IK=IC
=>I nằm trên đường trung trực của CK(3)
Từ (1),(2),(3) suy ra A,D,I thẳng hàng