Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
1) \(x^2-4x+4=\left(x-2\right)^2\)
2) \(x^2-9=x^2-3^2=\left(x-3\right)\left(x+3\right)\)
3) \(1-8x^3=\left(1-2x\right)\left(1+2x+4x^2\right)\)
4) \(\left(x-y\right)^2-9x^2=\left(x-y\right)^2-\left(3x\right)^2=\left(x-y-3x\right)\left(x-y+3x\right)=\left(-2x-y\right)\left(4x-y\right)\)
5) \(\dfrac{1}{25}x^2-64y^2=\left(\dfrac{1}{5}x-8y\right)\left(\dfrac{1}{5}x+8y\right)\)
6) \(8x^3-\dfrac{1}{8}=\left(2x-\dfrac{1}{2}\right)\left(4x^2+x+\dfrac{1}{4}\right)\)

Câu 1:
Nhân từng hạng tử của đa thức/đơn thức này cho từng hạng tử của đa thức/đơn thức kia. Sau đó, thu gọn lại ta được kết quả cần tìm
Câu 2:
Có 7 hằng đẳng thức. Công thức:
1: \(\left(a+b\right)^2=a^2+2ab+b^2\)
2: \(\left(a-b\right)^2=a^2-2ab+b^2\)
3: \(a^2-b^2=\left(a-b\right)\left(a+b\right)\)
4: \(\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3\)
5: \(\left(a-b\right)^3=a^3-3a^2b+3ab^2-b^3\)
6: \(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)\)
7: \(a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)\)

Bài 1:
\(1,Sửa:x^3-2x^2+x=x\left(x^2-2x+1\right)=x\left(x-1\right)^2\\ 2,=6\left(x^2+2xy+y^2\right)=6\left(x+y\right)^2\\ 3,=2y\left(y^2+4y+4\right)=2y\left(y+2\right)^2\\ 4,=5\left(x^2-2xy+y^2\right)=5\left(x-y\right)^2\)
Bài 2:
\(1,=x\left(x^2-64\right)=x\left(x-8\right)\left(x+8\right)\\ 2,=2y\left(4x^2-9\right)=2y\left(2x-3\right)\left(2x+3\right)\\ 3,=3\left(x^3-1\right)=3\left(x-1\right)\left(x^2+x+1\right)\)
Bài 3:
\(a,=5\left(x^2+2x+1-y^2\right)=5\left[\left(x+1\right)^2-y^2\right]=5\left(x-y+1\right)\left(x+y+1\right)\\ b,=3x\left(x^2-2x+1-4y^2\right)=3x\left[\left(x-1\right)^2-4y^2\right]\\ =3x\left(x-2y-1\right)\left(x+2y-1\right)\\ c,=ab\left(a-b\right)\left(a+b\right)+\left(a+b\right)^2\\ =\left(a+b\right)\left(a^2b-ab^2+a+b\right)\\ d,=2x\left(x^2-y^2-4x+4\right)=2x\left[\left(x-2\right)^2-y^2\right]\\ =2x\left(x-y-2\right)\left(x+y-2\right)\)

\(81x^2-y^2=\left(9x\right)^2-y^2\)\(=\left(9x-y\right)\left(9x+y\right)\)

\(10x-25-x^2=-\left(x^2-10x+25\right)\)
\(=-\left(x^2-2.x.5+5^2\right)=-\left(x-5\right)^2\)

1.a) (3x+1)2-4(x-2)2= (3x+1)2-[2(x-2)]2=[(3x+1)-2(x-2)][(3x+1)+2(x-2)]=(x+3)(5x-1)
b) (a2+b2-5)2-4(ab+2)2= (a2+b2-5)2-[2(ab+2)]2 = (a2+b2-5-2ab-4)(a2+b2-5+2ab+4)=[(a-b)2-9][(a+b)2-1]
2. 3x2+9x-30=3x2-6x+15x-30=3x(x-2)+15(x-2)=3(x+5)(x-2)
b. x3-5x2-14x=x3+2x2-7x2-14x=x2(x+2)-7x(x+2)=(x2-7x)(x+2)
a) \(\left(3x+1\right)^2-4\left(x-2\right)^2\)
\(=\left(3x+1\right)^2-\left[2.\left(x-2\right)\right]^2\)
\(=\left(3x+1\right)^2-\left(2x-4\right)^2\)
\(=\left[3x+1-2x+4\right].\left[3x+1+2x-4\right]\)
\(=\left(x+5\right)\left(5x-3\right)\)
b) \(\left(a^2+b^2-5\right)^2-4\left(ab+2\right)^2\)
\(=\left(a^2+b^2-5\right)^2-\left[2.\left(ab+2\right)\right]^2\)
\(=\left(a^2+b^2-5\right)^2-\left(2ab+4\right)^2\)
\(=\left(a^2+b^2-5-2ab-4\right)\left(a^2+b^2-5+2ab+4\right)\)
\(=\left[\left(a-b\right)^2-9\right].\left[\left(a+b\right)^2-1\right]\)
\(=\left[\left(a-b-3\right)\left(a-b+3\right)\right].\left[\left(a+b-1\right)\left(a+b+1\right)\right]\)
a) \(3x^2+9x-30\)
\(=3\left(x^2+3x-10\right)\)
\(=3\left(x^2-2x+5x-10\right)\)
\(=3.\left[x\left(x-2\right)+5.\left(x-2\right)\right]\)
\(=3.\left[\left(x+5\right)\left(x-2\right)\right]\)
b) \(x^3-5x^2-14x\)
\(=x\left(x^2-5x-14\right)\)
\(=x\left(x^2+2x-7x-14\right)\)
\(=x.\left[x\left(x+2\right)-7.\left(x+2\right)\right]\)
\(=x.\left[\left(x-7\right)\left(x+2\right)\right]\)

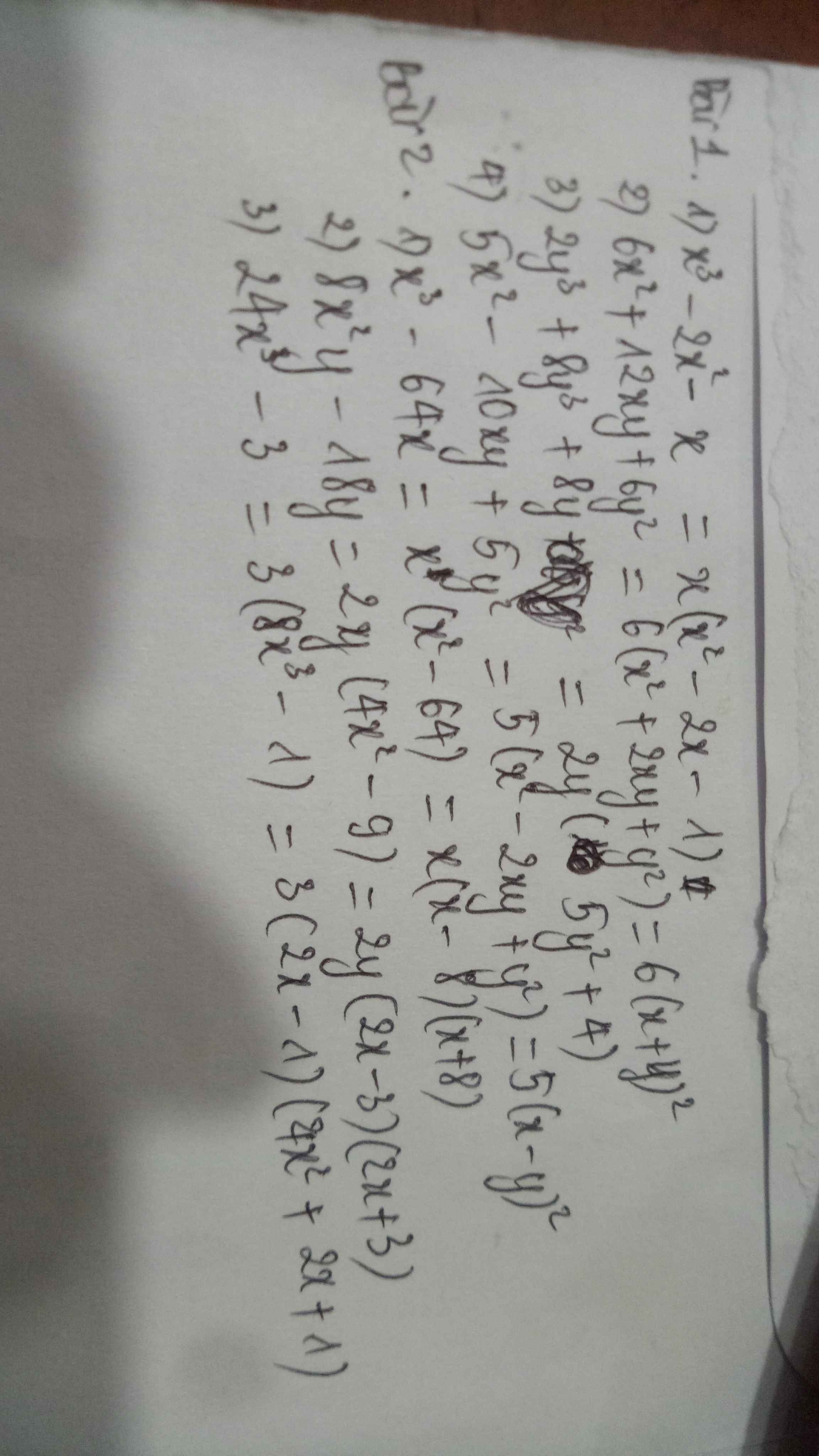
*Dạng tổng quát của 7 hằng đẳng thức đáng nhớ
1: \(\left(a+b\right)^2=a^2+2ab+b^2\)
2: \(\left(a-b\right)^2=a^2-2ab+b^2\)
3: \(a^2-b^2=\left(a-b\right)\left(a+b\right)\)
4: \(\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3\)
5: \(\left(a-b\right)^3=a^3-3a^2b+3ab^2-b^3\)
6: \(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)\)
7: \(a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)\)
*Các phương pháp phân tích đa thức thành nhân tử
1: Phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung
2: Phân tích đa thức thành nhân tử bằng cách dùng hằng đẳng thức
3: Phân tích đa thức thành nhân tử bằng cách nhóm nhiều hạng tử
4: Phân tích đa thức thành nhân tử bằng cách tách hạng tử
5: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp