Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đầu tiên coi các quả là khác nhau. Do vậy có 9! cách chia.
Nhưng các quả cùng loại (táo, cam, chuối) là giống nhau nên nếu các cháu có cùng loại quả đổi cho nhau thì vẫn chỉ là một cách chia. Vì vậy, số cách chia là:
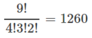
Có thể giải theo các cách như sau:
Chọn 4 trong 9 cháu để phát táo. Có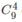 
cách.
Chọn 3 trong 5 cháu còn lại để phát cam. Có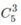 
cách.
Chuối sẽ phát cho 2 cháu còn lại.
Vậy có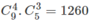 
cách.
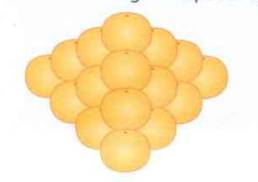
Ta sử dụng phương pháp thử và sai, bắt đầu với n = 1 và tăng giá trị của n cho đến khi 1/6n(n+1)(n+2) vượt quá 100. Khi đó, n - 1 sẽ là số lớp tối đa của khối tứ diện.
Thử nghiệm:
- Với n = 1: 1/6 x 1 x 2 x 3 = 1, không vượt quá 100.
- Với n = 2: 1/6 x 2 x 3 x 4 = 4, không vượt quá 100.
- Với n = 3: 1/6 x 3 x 4 x 5 = 10, không vượt quá 100.
- Với n = 4: 1/6 x 4 x 5 x 6 = 20/3, vượt quá 100.
Vậy, số lớp tối đa của khối tứ diện được xếp từ 100 quả cam là n - 1 = 3.
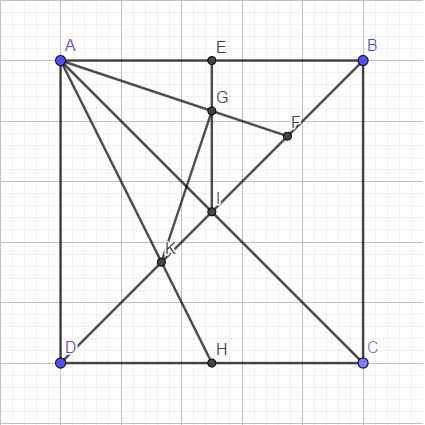
Đặt tên điểm như hình vẽ bên dưới
Ta có: F là trung điểm BI \(\Rightarrow\overrightarrow{AF}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AI}\right)\)
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AF}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AI}\right)=\dfrac{1}{3}\left(\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AC}\)
\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{6}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\)
\(\overrightarrow{AH}=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AC}=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AK}=\dfrac{2}{3}\overrightarrow{AH}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AD}\)
\(\overrightarrow{GK}=\overrightarrow{GA}+\overrightarrow{AK}=-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{6}\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AD}=-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AG}.\overrightarrow{GK}=\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\right)\left(-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\right)=-\dfrac{1}{12}AB^2+\dfrac{1}{12}AD^2=0\)
\(\Rightarrow AG\perp GK\)
\(\left\{{}\begin{matrix}\overrightarrow{GA}=\left(a+\dfrac{1}{3};b\right)\\\overrightarrow{KG}=\left(0;\dfrac{5}{3}\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{GA}.\overrightarrow{KG}=\left(a+\dfrac{1}{3}\right).0+\dfrac{5}{3}b=0\Rightarrow b=0\)
Mặt khác: \(AG^2-GK^2=\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\right)^2-\left(-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\right)^2=0\)
\(\Rightarrow AG^2=GK^2\Rightarrow\left(a+\dfrac{1}{3}\right)^2=\left(\dfrac{5}{3}\right)^2\Rightarrow a=-2\)
Lập phương trình
Gọi số trang là: x {hỏi cái gì đắt cái đó làm ẩn}
gọi số trang đọc theo đọc được theo từng ngày là: a[1,2,3]
thì ta có hệ phương trình:\(\left\{\begin{matrix}a_1+5=\frac{1}{5}x\\a_2-7=\left(x-a_1\right)\\a_3=\frac{2}{5}\left[x-\left(a_1+a_2\right)\right]\\a_4=\frac{2}{3}\left[x-\left(a_1+a_2+a_3\right)\right]\end{matrix}\right.\)
Thiếu 1 pt: \(\left(a_1+a_2+a_3+a_4+41\right)=x\) {không vào sửa được-> viết ngoài hệ}
Như vậy ta có hệ 5 pt 5 ẩn => đủ để tìm x, (bạn tự làm)
đọc lại đề nhầm ngày thứ 4 đọc hết quyển truyện {tương còn để lại 41}
do vây--> a4=2/3[...]+41
Phuowfg trình bên ngoài hệ còn (a1+a2+a3+a4)=x
Tổng số sách là: 15(quyển)
Chọn 1 quyển trong 15 quyển có \(C_{15}^1=15\) (cách chọn)
=>Cô Vân có 15 cách tặng sách
n(Ω)= C102=45
A:” lấy hai quả khác loại” thì n(A)= C51.C31+C51.C21+C21 C31=31.
Vậy P(A)=31/45
Chọn C
mình cũng nghĩ là có một cách nhưng cô cho đáp án là 105 cách áp dụng công thức tổ hợp
Bài 1:
\(A=\dfrac{1}{2}\left(\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+...+\dfrac{2}{2011\cdot2013}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{2011}-\dfrac{1}{2013}\right)\)
\(=\dfrac{1}{2}\cdot\left(\dfrac{1}{5}-\dfrac{1}{2013}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2008}{10065}=\dfrac{1004}{10065}\)
Bài 2:
Sau buổi sáng còn 1-1/3=2/3(tổng số)
Sau buổi chiều còn 2/3x5/8=10/24=5/12(tổng số)
Cô Vân mua về:
25:5/12=60(kg)