Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a. $=(x-y)(x+y)=[(-1)-(-3)][(-1)+(-3)]=2(-4)=-8$
b. $=3x^4-2xy^3+x^3y^2+3x^2y+12xy+15y-12xy-12$
$=3x^4-2xy^3+x^3y^2+3x^2y+15y-12$
=3-2.1(-2)^3+1^3.(-2)^2+3.1^2(-2)+15(-2)-12$
$=-25$
c.
$=2x^4+3x^3y-4x^3y-12xy+12xy=2x^4-x^3y$
$=x^3(2x-y)=(-1)^3[2(-1)-2]=-1.(-4)=4$
d.
$=2x^2y+4x^2-5xy^2-10x+3xy^2-3x^2y$
$=(2x^2y-3x^2y)+4x^2+(-5xy^2+3xy^2)-10x$
$=-x^2y+4x^2-2xy^2-10x$
$=-3^2.(-2)+4.3^2-2.3(-2)^2-10.3=0$

a: Ta có: \(x^2-4x\left(3x-4\right)+7x-5\)
\(=x^2-12x^2+16x+7x-5\)
\(=-11x^2+23x-5\)
b: Ta có: \(7x\left(x^2-5\right)-3x^2y\left(xy-6y^2\right)\)
\(=7x^3-35x-3x^3y^2+18x^2y^3\)
c: Ta có: \(\left(5x+4\right)\left(2x-7\right)\)
\(=10x^2-35x+8x-28\)
\(=10x^2-27x-28\)

a) 5x2 ( 3x2 -7x+2)-15x(x-3)
=15x4-35x3+10x2-15x2+45x
=15x4-35x3-5x2+45x
c) (x+3)(x-3)(x-2)(x+1)
=(x2-9)(x2+x-2x-2)
=(x2-9)(x2-x-2)
=x4-x3-2x2-9x2+9x+18
=x4-x3-11x2+9x+18
d)(2x+1)2+(4x-1)2+2(2x+1)(4x+1)
=2x2+4x+1-16x2-8x+1
=2x2+4x+1-16x2-8x+1+16x2-4x+8x-2
=2x2+7
e) (2x2-3x)(5x2-2x+1)-10x2(x+3)
=10x4 -4x3+2x2-15x3+6x2-3 -10x2-30x
=10x4-19x3-2x2-30x-3

Bài 1:
a: ĐKXĐ: \(x+4\ne0\)
=>\(x\ne-4\)
b: ĐKXĐ: \(2x-1\ne0\)
=>\(2x\ne1\)
=>\(x\ne\dfrac{1}{2}\)
c: ĐKXĐ: \(x\left(y-3\right)\ne0\)
=>\(\left\{{}\begin{matrix}x\ne0\\y-3\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne0\\y\ne3\end{matrix}\right.\)
d: ĐKXĐ: \(x^2-4y^2\ne0\)
=>\(\left(x-2y\right)\left(x+2y\right)\ne0\)
=>\(x\ne\pm2y\)
e: ĐKXĐ: \(\left(5-x\right)\left(y+2\right)\ne0\)
=>\(\left\{{}\begin{matrix}x\ne5\\y\ne-2\end{matrix}\right.\)
Bài 2:
a: \(\dfrac{-12x^3y^2}{-20x^2y^2}=\dfrac{12x^3y^2}{20x^2y^2}=\dfrac{12x^3y^2:4x^2y^2}{20x^2y^2:4x^2y^2}=\dfrac{3x}{5}\)
b: \(\dfrac{x^2+xy-x-y}{x^2-xy-x+y}\)
\(=\dfrac{\left(x^2+xy\right)-\left(x+y\right)}{\left(x^2-xy\right)-\left(x-y\right)}\)
\(=\dfrac{x\left(x+y\right)-\left(x+y\right)}{x\left(x-y\right)-\left(x-y\right)}=\dfrac{\left(x+y\right)\left(x-1\right)}{\left(x-y\right)\left(x-1\right)}\)
\(=\dfrac{x+y}{x-y}\)
c: \(\dfrac{7x^2-7xy}{y^2-x^2}\)
\(=\dfrac{7x\left(x-y\right)}{\left(y-x\right)\left(y+x\right)}\)
\(=\dfrac{-7x\left(x-y\right)}{\left(x-y\right)\left(x+y\right)}=\dfrac{-7x}{x+y}\)
d: \(\dfrac{7x^2+14x+7}{3x^2+3x}\)
\(=\dfrac{7\left(x^2+2x+1\right)}{3x\left(x+1\right)}\)
\(=\dfrac{7\left(x+1\right)^2}{3x\left(x+1\right)}=\dfrac{7\left(x+1\right)}{3x}\)
e: \(\dfrac{3y-2-3xy+2x}{1-3x-x^3+3x^2}\)
\(=\dfrac{3y-2-x\left(3y-2\right)}{1-3x+3x^2-x^3}\)
\(=\dfrac{\left(3y-2\right)\left(1-x\right)}{\left(1-x\right)^3}=\dfrac{3y-2}{\left(1-x\right)^2}\)
g: \(\dfrac{x^2+7x+12}{x^2+5x+6}\)
\(=\dfrac{\left(x+3\right)\left(x+4\right)}{\left(x+3\right)\left(x+2\right)}\)
\(=\dfrac{x+4}{x+2}\)

Bài 3:
3: \(6x\left(x-y\right)-9y^2+9xy\)
\(=6x\left(x-y\right)+9xy-9y^2\)
\(=6x\left(x-y\right)+9y\left(x-y\right)\)
\(=\left(x-y\right)\left(6x+9y\right)\)
\(=3\left(2x+3y\right)\left(x-y\right)\)
Bài 4:




1)2xy+3z+6y+xz
= x(2y + z) + 3(z + 2y)
= (x + 3)(2y + z)
2)x^4-9x^3+x^2-9x
= x^2(x^2 + 1) - 9x(x^2 + 1)
= (x^2 + 1)(x^2 - 9x)
= x(x - 9)(x^2 + 1)
3)x^2-xy+x-y
= x(x - y) + (x - y)
= (x + 1)(x - y)
4)xz+yz-5(x+y)
= z(x + y) - 5(x + y)
= (z - 5)(x + y)
5)3x^2-3xy-5x+5y
= 3x(x - y) - 5(x - y)
= (3x - 5)(x - y)
6)x^2+4x-y^2+4y
= (x - y)(x + y) + 4(x + y)
= (x - y + 4)(x + y)

1.
\(a,\left(-xy\right)\left(-2x^2y+3xy-7x\right)\)
\(=2x^3y^2-3x^2y^2+7x^2y\)
\(b,\left(\dfrac{1}{6}x^2y^2\right)\left(-0,3x^2y-0,4xy+1\right)\)
\(=-\dfrac{1}{20}x^4y^3-\dfrac{1}{15}x^3y^3+\dfrac{1}{6}x^2y^2\)
\(c,\left(x+y\right)\left(x^2+2xy+y^2\right)\)
\(=\left(x+y\right)^3\)
\(=x^3+3x^2y+3xy^2+y^3\)
\(d,\left(x-y\right)\left(x^2-2xy+y^2\right)\)
\(=\left(x-y\right)^3\)
\(=x^3-3x^2y+3xy^2-y^3\)
2.
\(a,\left(x-y\right)\left(x^2+xy+y^2\right)\)
\(=x^3-y^3\)
\(b,\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(=x^3+y^3\)
\(c,\left(4x-1\right)\left(6y+1\right)-3x\left(8y+\dfrac{4}{3}\right)\)
\(=24xy+4x-6y-1-24xy-4x\)
\(=\left(24xy-24xy\right)+\left(4x-4x\right)-6y-1\)
\(=-6y-1\)
#Toru

1) 2x + 2y - x(x+y)
= 2(x + y) - x(x + y)
= (2 - x)(x + y)
2/ 5x2 - 5xy -10x + 10y
= 5x(x - y) - 10(x - y)
= (5x - 10(x - y)
3/ 4x2 + 8xy - 3x - 6y
= 4x(x + 2y) - 3(x + 2y)
= (4x - 3)(x + 2y)
1) 2x + 2y - x(x + y)
= 2(x + y) - x(x + y)
= (2 - x)(x + y)
2) 5x2 - 5xy - 10x + 10y
= 5x(x - y) - 10(x - y)
= (5x - 10)(x - y)
= 5(x - 2)(x - y)
3) 4x2 + 8xy - 3x - 6y
= 4x(x + 2y) - 3(x + 2y)
= (4x - 3)(x + 2y)
4) 2x2 + 2y2 - x2z + z - y2z - 2
= 2(x2 + y2 - z(x2 + y2) - (2 - z)
= (2 - z)(x2 + y2) - (2 - z)
= (2 - z)(x2 + y2)
5) x2 + xy - 5x - 5y
= x(x + y) - 5(x + y)
= (x - 5)(x + y)
6) x(2x - 7) - 4x + 14
= x(2x - 7) - 2(2x - 7)
= (x - 2)(2x - 7)
7)x2 - 3x + xy - 3y
= x(x + y) - 3(x + y)
= (x - 3)(x + y)
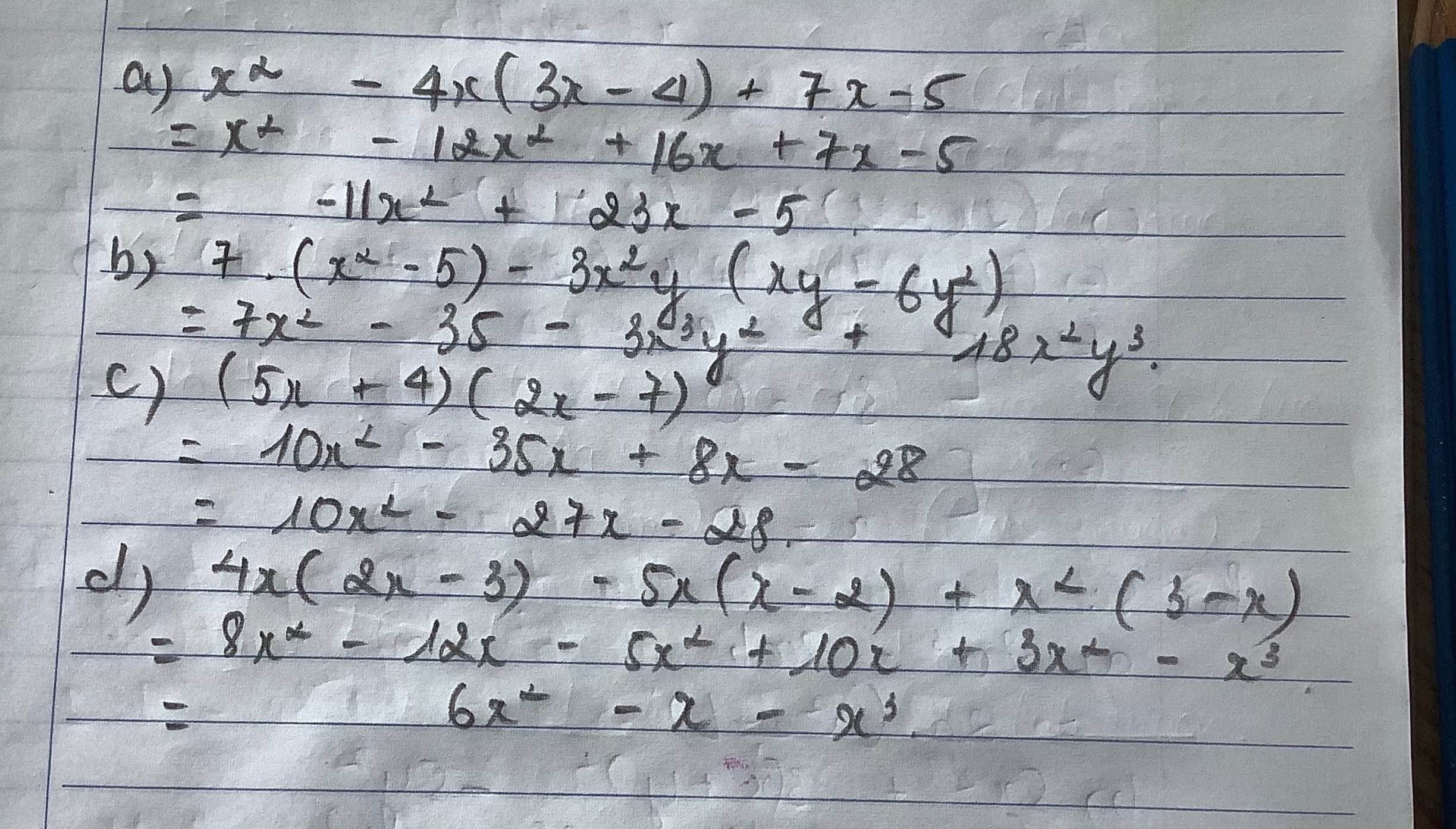



Bài 1 :
a, sai đề
b, \(\frac{x^2-xy-x+y}{x^2+xy-x-y}=\frac{x\left(x-y\right)-\left(x-y\right)}{x\left(x+y\right)-\left(x+y\right)}=\frac{\left(x-1\right)\left(x-y\right)}{\left(x-1\right)\left(x+y\right)}=\frac{x-y}{x+y}\)
Bài 2 :
a, \(\frac{3x-7x}{3x-5x}-\frac{4x-7}{3x-5}=2-\frac{4x-7}{3x-5}=\frac{2\left(3x-5\right)-4x-7}{3x-5}\)
\(=\frac{6x-10-4x-7}{3x-5}=\frac{2x-17}{3x-5}\)
b, \(\frac{x^3-1}{x^3+x^2+x}-\frac{x^2-4}{6y-3xy}=\frac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x^2+x+1\right)}-\frac{\left(x-2\right)\left(x+2\right)}{3y\left(2-x\right)}\)
\(=\frac{x-1}{x}-\frac{-\left(2-x\right)\left(x+2\right)}{3y\left(2-x\right)}=\frac{x-1}{x}+\frac{x+2}{3y}\)