Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A P B M D C F E N H 1 1 2 1 2 O
1. Xét tứ giác CEHD ta có:
Góc CEH = 900 (Vì BE là đường cao)
Góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEC = 900.
CF là đường cao => CF ┴ AB => góc BFC = 900.
Như vậy E và F cùng nhìn BC dưới một góc 900 => E và F cùng nằm trên đường tròn đường kính BC.
Vậy bốn điểm B,C,E,F cùng nằm trên một đường tròn.
3. Xét hai tam giác AEH và ADC ta có: góc AEH = góc ADC = 900; góc A là góc chung
=> Δ AEH ˜ Δ ADC => AE/AD = AH/AC=> AE.AC = AH.AD.
* Xét hai tam giác BEC và ADC ta có: góc BEC = góc ADC = 900; góc C là góc chung
=> Δ BEC ˜ Δ ADC => AE/AD = BC/AC => AD.BC = BE.AC.
4. Ta có góc C1 = góc A1 (vì cùng phụ với góc ABC)
góc C2 = góc A1 ( vì là hai góc nội tiếp cùng chắn cung BM)
=> góc C1 = góc C2 => CB là tia phân giác của góc HCM; lại có CB ┴ HM => Δ CHM cân tại C
=> CB cũng là đương trung trực của HM vậy H và M đối xứng nhau qua BC.
5. Theo chứng minh trên bốn điểm B, C, E, F cùng nằm trên một đường tròn
=> góc C1 = góc E1 (vì là hai góc nội tiếp cùng chắn cung BF)
Cũng theo chứng minh trên CEHD là tứ giác nội tiếp
góc C1 = góc E2 (vì là hai góc nội tiếp cùng chắn cung HD)
góc E1 = góc E2 => EB là tia phân giác của góc FED.
Chứng minh tương tự ta cũng có FC là tia phân giác của góc DFE mà BE và CF cắt nhau tại H do đó H là tâm đường tròn nội tiếp tam giác DEF.
APBMDCFENH11212O
1. Xét tứ giác CEHD ta có:
Góc CEH = 900 (Vì BE là đường cao)
Góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEC = 900.
CF là đường cao => CF ┴ AB => góc BFC = 900.
Như vậy E và F cùng nhìn BC dưới một góc 900 => E và F cùng nằm trên đường tròn đường kính BC.
Vậy bốn điểm B,C,E,F cùng nằm trên một đường tròn.
3. Xét hai tam giác AEH và ADC ta có: góc AEH = góc ADC = 900; góc A là góc chung
=> Δ AEH ˜ Δ ADC => AE/AD = AH/AC=> AE.AC = AH.AD.
* Xét hai tam giác BEC và ADC ta có: góc BEC = góc ADC = 900; góc C là góc chung
=> Δ BEC ˜ Δ ADC => AE/AD = BC/AC => AD.BC = BE.AC.
4. Ta có góc C1 = góc A1 (vì cùng phụ với góc ABC)
góc C2 = góc A1 ( vì là hai góc nội tiếp cùng chắn cung BM)
=> góc C1 = góc C2 => CB là tia phân giác của góc HCM; lại có CB ┴ HM => Δ CHM cân tại C
=> CB cũng là đương trung trực của HM vậy H và M đối xứng nhau qua BC.
5. Theo chứng minh trên bốn điểm B, C, E, F cùng nằm trên một đường tròn
=> góc C1 = góc E1 (vì là hai góc nội tiếp cùng chắn cung BF)
Cũng theo chứng minh trên CEHD là tứ giác nội tiếp
góc C1 = góc E2 (vì là hai góc nội tiếp cùng chắn cung HD)
góc E1 = góc E2 => EB là tia phân giác của góc FED.
Chứng minh tương tự ta cũng có FC là tia phân giác của góc DFE mà BE và CF cắt nhau tại H do đó H là tâm đường tròn nội tiếp tam giác DEF.

1. Xét tứ giác CEHD ta có:
Góc CEH = 900 (Vì BE là đường cao)
Góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEC = 900.
CF là đường cao => CF ┴ AB => góc BFC = 900.
Như vậy E và F cùng nhìn BC dưới một góc 900 => E và F cùng nằm trên đường tròn đường kính BC.
Vậy bốn điểm B,C,E,F cùng nằm trên một đường tròn.
3. Xét hai tam giác AEH và ADC ta có: góc AEH = góc ADC = 900; góc A là góc chung
=> Δ AEH ˜ Δ ADC => AE/AD = AH/AC=> AE.AC = AH.AD.
* Xét hai tam giác BEC và ADC ta có: góc BEC = góc ADC = 900; góc C là góc chung
=> Δ BEC ˜ Δ ADC => AE/AD = BC/AC => AD.BC = BE.AC.
4. Ta có góc C1 = góc A1 (vì cùng phụ với góc ABC)
góc C2 = góc A1 ( vì là hai góc nội tiếp cùng chắn cung BM)
=> góc C1 = góc C2 => CB là tia phân giác của góc HCM; lại có CB ┴ HM => Δ CHM cân tại C
=> CB cũng là đương trung trực của HM vậy H và M đối xứng nhau qua BC.
5. Theo chứng minh trên bốn điểm B, C, E, F cùng nằm trên một đường tròn
=> góc C1 = góc E1 (vì là hai góc nội tiếp cùng chắn cung BF)
Cũng theo chứng minh trên CEHD là tứ giác nội tiếp
góc C1 = góc E2 (vì là hai góc nội tiếp cùng chắn cung HD)
góc E1 = góc E2 => EB là tia phân giác của góc FED.
Chứng minh tương tự ta cũng có FC là tia phân giác của góc DFE mà BE và CF cắt nhau tại H do đó H là tâm đường tròn nội tiếp tam giác DEF.

\(VT=\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
\(=a^2c^2+2abcd+b^2d^2+a^2d^2-2abcd+b^2c^2\)
\(=a^2\left(c^2+d^2\right)+b^2\left(c^2+d^2\right)\)
\(=\left(a^2+b^2\right)\left(c^2+d^2\right)\)

Bài 1 ( của toán lớp 10 mà )
Ta có : ( P ) đi qua điểm A nên thay x = 4 ; y = 5 vào ( P ) , ta được :
5 = a . 42 + b . 4 + c
5 = 16a + 4b + c
-c = 16a + 4b - 5
=> c = -16a - 4b + 5 ( * )
( P ) có đỉnh là I(2;1)
=> \(\hept{\begin{cases}-\frac{b}{2a}=2\\-\frac{\Delta}{4a}=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}-b=4a\\-\frac{\left(b^2-4ac\right)}{4a}=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}b=-4a\\b^2-4ac=-4a\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}b=-4a\\b^2-4a.\left(-16a-4b+5\right)=-4a\end{cases}}\) ( c = - 16a -4b + 5 ) mình chứng minh ở trên nhé
\(\Leftrightarrow\hept{\begin{cases}b=-4a\\\left(-4a\right)^2-4a.\left(-16a-4\left(-4a\right)+5\right)=-4a\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}b=-4a\\16a^2+48a^2-48a^2-20a+4a=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}b=-4a\\16a^2-16a=0\end{cases}}\) ( ở bước này bạn có thể tính bằng tay hoặc dùng máy tính nha : more 5 - 3 )
\(\Leftrightarrow\hept{\begin{cases}b=-4a\\a=1\left(nhan\right);a=0\left(loai\right)\end{cases}}\) ( a = 0 thì loại ; vì trong phương trình bậc 2 thì a phải khác 0 )
\(\Leftrightarrow\hept{\begin{cases}a=1\\b=-4.\left(1\right)\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a=1\\b=-4\end{cases}}\)
Thay a = 1 và b = -4 vào phương trình ( * ) ta được :
c = -16 . 1 - 4 .( -4 ) +5 = 5
vậy ( P ) là \(y=x^2-4x+5\)
bảng biến thiên :
bạn tự vẽ (P) nha , quá dễ mà
BÀI 2 : \(\forall x\in R\) có nghĩa là vô số nghiệm
\(\left(m^2-1\right)x+2m=5x-2v6\)
\(\Leftrightarrow\left(m^2-1\right)x-5x=2v6-2m\)
\(\Leftrightarrow\left(m^2-1-5\right)x=2v6-2m\)
\(\Leftrightarrow\left(m^2-6\right)x=2v6-2m\)
Phương trình có nghiệm \(\forall x\in R\) \(\Leftrightarrow0x=0\)
\(\Leftrightarrow\hept{\begin{cases}m^2-6=0\\2v6-2m=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=\pm v6\\m=v6\end{cases}}\)
Vậy m = v6 thì phương trình có nghiệm đúng \(\forall x\in R\) ( bởi vì m = v6 và m =+-v6 nên ta chỉ lấy phần chung thôi ,lấy v6 ,loại bỏ -v6)
Bài 3 :
a )
\(\Delta=b^2-4ac\)
\(=\left[-2\left(2m-3\right)\right]^2-4.\left(2m-1\right).\left(2m+5\right)\)
\(=4.\left(4m^2-12m+9\right)-\left(8m-4\right)\left(2m+5\right)\)
\(=16m^2-12m+36-\left(16m^2+40m-8m-20\right)\)
\(=16m^2-12m+36-16m^2-40m+8m+20\)
\(=-44m+56\)
phương trình có nghiệm \(\Leftrightarrow\Delta\ge0\)
\(\Leftrightarrow-44m+56\ge0\)
\(\Leftrightarrow-44m\ge-56\)
\(\Leftrightarrow m\le\frac{14}{11}\)
Vậy \(m\le\frac{14}{11}\) thì phương trình có nghiệm ( m bé hơn hoặc bằng 14/11 nha )
b ) x1 = x2 có nghĩa là nghiệm kép nha ( có 2 nghiệm phân biệt x1,x2 ; đề bài đang đánh lừa bạn đấy )
phương trình có 2 nghiệm x1 = x2 \(\Leftrightarrow\Delta=0\)
\(\Leftrightarrow-44m+56=0\)
\(\Leftrightarrow m==\frac{14}{11}\)
Học tốt !!!!!
\(\Leftrightarrow\hept{\begin{cases}b=-4a\\\orbr{\begin{cases}a=0\\16a-16=0\end{cases}}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}b=-4a\\\orbr{\begin{cases}a=0\\16a-16=0\end{cases}}\end{cases}}\)

Câu hỏi của Mafia - Toán lớp 9 - Học toán với OnlineMath
Em có thể tham khảo tại đây nhé, bài này chỉ đơn giản là đổi tên điểm.

Ta có \(x^2-\left(7+y\right)x+6+2y=0\Leftrightarrow y\left(x-2\right)=x^2-7x+6\)
Rõ ràng x=2 không thể là nghiệm nên chia cả 2 vế cho x-2 ta được
\(y=\frac{x^2-7x+6}{x-2}=\left(x-5\right)+\frac{-4}{x-2}\)
Do x,y nguyên nên x-2 là Ư(-4) mà \(Ư_{\left(-4\right)}=\left\{-4;-2;-1;1;2;4\right\}\)
ta có bảng
| x-2 | -4 | -2 | -1 | 1 | 2 | 4 |
| x | -2 | 0 | 1 | 3 | 4 | 6 |
| y | 0 | -3 | -6 | 0 | -3 | 6 |
đối chiếu điều kiện ở đề bài thì các cặp
(x;y)={(1;0);(0;3);(-2;-6);(6;0);(4;-3);(3;-6)}


Đáp án:
Giải thích các bước giải:
1. Xét tứ giác CEHD có :
CEH = 90 ( BE là đường cao )
CDH = 90 ( AD là đường cao )
⇒ CEH + CDH = 90 + 90 = 180
Mà CEH và CDH là hai góc đối của tứ giác CEHD
⇒ CEHD là tứ giác nội tiếp (đpcm)
2. BE là đường cao ( gt )
⇒ BE ⊥ AB ⇒ BFC = 90
Như vậy E và F cùng nhìn BC dưới một góc 90 ⇒ E và F cùng nằm trên (O) đường kính AB
⇒ 4 điểm B, C, E, F cùng nằm trên một đường tròn (đpcm)
3. Xét ΔAEH và ΔADC có :
AEH = ADC (=90)
A chung
⇒ ΔAEH ~ ΔADC
⇒ AE/AD = AH/AC
⇒ AE.AC = AH.AD
Xét ΔBEC và ΔADC có :
BEC = ADC (=90)
C chung
⇒ ΔBEC ~ ΔADC
⇒ AE/AD = BC/AC
⇒ AD.BC = BE.AC (đpcm)
4. Có : C1 = A1 (cùng phụ góc ABC)
C2 = A1 ( hai góc nối tiếp chắn cung BM )
⇒ C1 = C2 ⇒ CB là tia phân giác HCM
Lại có : CB ⊥ HM
⇒ Δ CHM cân tại C
⇒ CB là đường trung trực của HM
⇒ H và M đối xứng nhau qua BC (đpcm)
5. Có : Bốn điểm B,C,E,F cùng nằm trên một đường tròn ( câu 2 )
⇒ C1 = E1 (hai góc nội tiếp cùng chắn BF) (*)
Có : Tứ giác CEHD nội tiếp (câu 1)
⇒ C1 = E2 (hai góc nội tiếp cùng chắn cung HD ) (**)
Từ (*) và (**) ta suy ra :
E1 = E2
⇒ EB là tia phân giác DEF
Cm tương tự ta được : FC là tia phân giác của DFE
Mà BE và CF cắt nhau tại H
⇒ H là tâm của đường tròn nội tiếp ΔDEF
Bài 3:
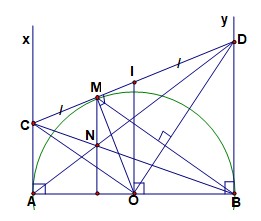
1. Vì CM,CA là tiếp tuyến của (O)
\(\rightarrow OC\) là phân giác \(\widehat{AOM},CM=CA\)
Tương tự \(OD\) là phân giác \(\widehat{BOM},DM=DB\)
\(\rightarrow AC+BD=CM+DM=DB\)
2. Từ câu 1:
\(\rightarrow\widehat{COD}=\widehat{COM}+\widehat{MOD}=\frac{1}{2}\widehat{AOM}+\frac{1}{2}\widehat{MOB}=90^o\)
3. Ta có:
\(OC\perp OD,OM\perp CD\rightarrow CM.DM=OM^2\)
Mà \(AC=CM,DM=DB,OM=R\rightarrow AC.BD=R^2=\frac{AB^2}{4}\)
4. Vì \(CA,CM\) là tiếp tuyến của (O)
\(\rightarrow OC\perp AM\)
Mà \(AM\perp BM\) vì AB là đường kính của (O)
\(\rightarrow OC//BM\)
5. Lấy I là trung điểm CD vì \(\widehat{COD}=90^o\rightarrow\left(I,IO\right)\) là đường tròn đường kính CD
Mà O là trung điểm AB, \(AC//DB\left(\perp AB\right)\)
\(\rightarrow IO\) là đường trung bình hình thang \(\text{◊}ABCD\)
\(\rightarrow IO//AC\rightarrow IO\perp AB\)
\(\rightarrow AB\) là tiếp tuyến của (I,IO)
Hay AB là tiếp tuyến của đường tròn đường kính CD
6. Ta có : \(AC//BD,CM,CA,DM,DA\)
\(\rightarrow\frac{NA}{ND}=\frac{AC}{BD}=\frac{CM}{MD}\)
\(MN//AC\rightarrow MN\perp AB\left(AC\perp AB\right)\)
7. Để \(ABCD\) có chu vi nhỏ nhất
\(\rightarrow AB+BD+AC+CD\) nhỏ nhất
\(\rightarrow AB+CD+CD\) nhỏ nhất
\(\rightarrow AB+2CD\) nhỏ nhất
\(\rightarrow CD\) nhỏ nhất
Mà \(CD\ge AB\) vì \(ABCD\) là hình thang vuông tại A,B
Dấu = xảy ra khi \(CD//AB\rightarrow M\) nằm giữa A và B