Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải
Vì E là trung điểm AC
F là trung điểm BD
=> EF // CD // AB
=>góc AEF \(\perp\) CEF vuông
Xét \(\Delta\) AEF và CEF có
:/\ AEF = /\ CEF = 90 độ
EF chung
AE = AC (gt)
=> \(\Delta\) AEF = CEF ( cạnh góc cạnh )
=>\(\Delta\) AFD là tam giác cân
b, Vì \(\Delta\)AFD là \(\Delta\)cân nên
\(\Rightarrow\)Góc FAD = góc FDA
Ta có : góc A = góc BAF + góc FAD
Góc D = góc CDF + góc FDA
mà góc A = góc D = 90 độ
=> góc BAF = góc CDF

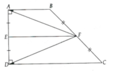
A B C D . E F Giải E là trung điểm AC F là trung điểm BD => EF // CD // AB => góc AEF vuông góc CEF vuông Xét tam giác AEF và CEF có : /\ AEF = /\ CEF = 90 độ EF chung AE = AC (gt) => tam giác AEF = CEF ( cạnh góc cạnh ) => FA = FC => tam giác AFC cân tại F ( đpcm )

Hình thang ABCD có
E là trung điểm của AD
F là trung điểm của BC
Do đó: EF là đường trung bình của hình thang ABCD
Suy ra: EF//AB//CD
mà AB\(\perp\)AD
nên EF\(\perp\)AD
Xét ΔFAD có
FE là đường cao ứng với cạnh AD
FE là đường trung tuyến ứng với cạnh AD
Do đó: ΔFAD cân tại F
b) Ta có: \(\widehat{BAF}+\widehat{DAF}=90^0\)
\(\widehat{CDF}+\widehat{FDA}=90^0\)
mà \(\widehat{FAD}=\widehat{FDA}\)(ΔFAD cân tại F)
nên \(\widehat{BAF}=\widehat{CDF}\)

a) Ta có È là đường trung bình của hình thang ABCD.
Þ EF//AB.
Suy ra EF ^ AD
Khi đó EF vừa trung tuyến, vừa là đường cao của tam giác AFD Þ ĐPCM.
b) Tam giác AFD cân tại F nên E A F ^ = E D F ^
Suy ra F A B ^ = C D F ^

Có : ED = EB = BD/2 ; AF = CF = AC/2 .
⇒⇒ BDACBDAC = BD2CD2BD2CD2 = DECFDECF (1).
Gọi O là điểm giao của BD và AC .
Xét ΔΔ ABO có BD // AC , theo hệ quả của định lí Ta-lét
⇒⇒ DOBO=COAODOBO=COAO
⇒⇒ DODO+BO=COCO+AODODO+BO=COCO+AO ⇔⇔ DOBD=COACDOBD=COAC
⇒⇒ BDAC=DOCOBDAC=DOCO (2) .
Từ (1) và (2) ta đc : DECF=DOCODECF=DOCO
⇒⇒DOCO=DECF=DO−DECO−CF=OEOFDOCO=DECF=DO−DECO−CF=OEOF.
⇒⇒ OEOD=OFOCOEOD=OFOC
Xét ΔΔ OCD có :OEOD=OFOCOEOD=OFOC (c/m trên)
⇒⇒ EF // CD (định lí Ta-lét đảo) .
Mà KH ⊥⊥ EF ⇒⇒ KH ⊥⊥ CD .
Xét ΔΔ HCD có :
KH ⊥⊥ CD ; HC = HD
⇒⇒ ΔΔ HCD cân tại H (KH vừa là trung tuyến , vừa là đường cao của ΔΔ HCD ) .
cho k
A B C D E F
a, Vì E là trung điểm của AD => AE=ED=> EF là đường trung tuyến của tam giác AFD (1 )
Ta có : E là trung điểm AD, F là trung điểm BC => EF là đường trung bình của hình thang ABCD
=> EF//AB//DC
Vì EF//AB, AD_|_ AB => EF_|_AD=> EF là đường cao của tam giác AFD (2)
Ta có : AE=ED, EF_|_ AD => EF là đường trung trực của tam giác AFD (3)
Từ ( 1 ), (2), (3) => tam giác AFD cân tại F
b, Vì tam giác AFD cân tại F => \(\widehat{FAD}=\widehat{FDA}\)
Ta có : \(\widehat{A}=\widehat{BAF}+\widehat{FAD}\)
\(\widehat{D}=\widehat{CDF}+\widehat{FDA}\)
mà \(\widehat{A}=\widehat{D}=90^0\)
=> \(\widehat{BAF}=\widehat{CDF}\)