Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

:v Làm bài 31 thôi nhá , còn lại all tự làm -..-
Gọi x (cm) , y (cm) là độ dài hai cạnh góc vuông của tam giác vuông (x > 2, y > 4).
Diện tích tam giác ban đầu là \(\frac{1}{2}xy\left(cm^2\right)\)
+ Tăng mỗi cạnh lên 3cm thì tam giác vuông mới có độ dài 2 cạnh là x + 3(cm) và y + 3 (cm)
Diện tích tam giác mới là : \(\frac{1}{2}\left(x+3\right)\left(y+3\right)\left(cm^2\right)\)
Diện tích tăng thêm 36 cm2 nên ta có p/trình :
\(\frac{1}{2}\left(x+3\right)\left(y+3\right)=\frac{1}{2}xy+36\)
\(\Leftrightarrow\left(x+3\right)\left(y+3\right)=xy+72\)
\(\Leftrightarrow xy+3x+3y+9=xy+72\)
\(\Leftrightarrow3x+3y=63\)
\(\Leftrightarrow x+y=21\)
+ Giảm một cạnh 2cm và giảm cạnh kia 4cm thì tam giác vuông mới có 2 cạnh là : x – 2 (cm) và y – 4 (cm).
Diện tích tam giác mới là : \(\frac{1}{2}\left(x-2\right)\left(y-4\right)\left(cm^2\right)\)
Diện tích giảm đi 26cm2 nên ta có phương trình :
\(\frac{1}{2}\left(x-2\right)\left(y-4\right)=\frac{1}{2}xy-26\)
\(\Leftrightarrow\left(x-2\right)\left(y-4\right)=xy-52\)
\(\Leftrightarrow xy-4x-2y+8=xy-52\)
\(\Leftrightarrow4x+2y=60\)
\(\Leftrightarrow2x+y=30\)
Ta có hệ phương trình : \(\hept{\begin{cases}x+y=21\\2x+y=30\end{cases}}\)
Lấy phương trình thứ hai trừ phương trình thứ nhất ta được :
\(\hept{\begin{cases}\left(2x+y\right)-\left(x+y\right)=30-21\\x+y=21\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x+y-\left(x+y\right)=9\\x+y=21\end{cases}\Leftrightarrow\hept{\begin{cases}x=9\\y=12\end{cases}}}\)
Vậy tam giác có hai cạnh lần lượt là 9cm và 12cm

Tham khảo ạ!

O là trung điểm của CD
AB đi qua trung điểm của CD nhưng AB không vuông góc với CD

Ta có:
(sinC) ^ 2 + (cosC) ^ 2 = (AB / BC) ^ 2 + (AC / BC) ^ 2
=(AB ^ 2 + AC ^ 2) / BC ^ 2 = BC ^ 2 / BC ^ 2 = 1
(Vì ABC vuông tại A mà, nên theo pitago)
-->(cosC) ^ 2 = 1 - (sinC) ^ 2 = 1 - 0,8 ^ 2 = 0,36
--> cosC = 0,6 hoặc cosC = - 0,6 (loại vì C là 1 góc nhọn)
Vậy cosC = 0,6
tanC = 0,8 / 0,6 = 4 / 3, cotC = 0,6 / 0,8 = 0,75

\(A=0.5\cdot4\sqrt{3-x}-\sqrt{3-x}-2\sqrt{3}+1=\sqrt{3-x}-2\sqrt{3}+1\) (xác định khi x=<3)
a)thay \(x=2\sqrt{2}\)vào a ra có
\(\sqrt{3-2\sqrt{2}}-2\sqrt{3}+1=\sqrt{\left(\sqrt{2}-1\right)^2}-2\sqrt{3}+1\)
\(=\sqrt{2}-1+2\sqrt{3}+1=\sqrt{2}+2\sqrt{3}\)
Để A=1<=> \(\sqrt{3-x}-2\sqrt{3}+1=1\\ \Leftrightarrow\sqrt{3-x}-2\sqrt{3}+1-1=0\\ \Leftrightarrow\sqrt{3-x}-2\sqrt{3}=0\\ \Leftrightarrow3-x=12\Leftrightarrow x=-9\)
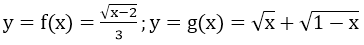
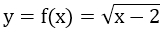 với x ≥ 2
với x ≥ 2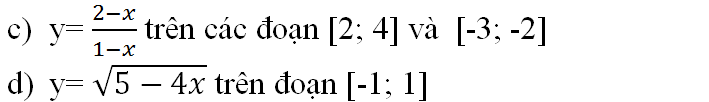

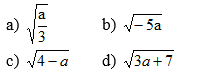
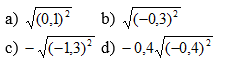


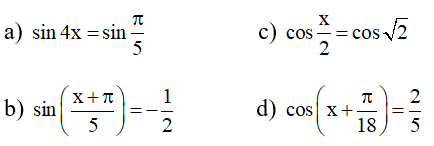
TL ;
Helppppppppppp ! Đang cần gấp
HT
TL
1.a: Tập xác định của y=f(x) là D=[2;+∞)
HT