Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi số cây của lớp 7A; 7B; 7C lần lượt là a; b; c (cây; a,c,b > 0)
ta có :
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)
\(\Rightarrow\frac{a+b+c}{3+4+5}=\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{180}{12}\)
\(\Rightarrow\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=15\)
\(\Rightarrow\hept{\begin{cases}a=15\cdot3=45\\b=15\cdot4=60\\c=15\cdot5=75\end{cases}}\)
Để cho tiện,ta gọi số cây của ba lớp trên lần lượt là: 7A,7B,7C
Theo đề bài,ta có: \(\frac{7A}{3}=\frac{7B}{4}=\frac{7C}{5}\)và \(7A+7B+7C=180\)
Áp dụng t/c dãy tỉ số bằng nhau ta có: \(\frac{7A}{3}=\frac{7B}{4}=\frac{7C}{5}=\frac{7A+7B+7C}{3+4+5}=\frac{180}{12}=15\)
Từ: \(\frac{7A}{3}=15\Rightarrow7A=15.3=45\)cây
\(\frac{7B}{4}=15\Rightarrow7B=15.4=60\) cây
\(\frac{7C}{5}=15\Rightarrow7C=75\) cây

Vậy lớp 7A trồng được 100 cây
lớp 7B trồng được 80 cây
lớp 7C trồng được 60 cây
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{240}{12}=20\)
Do đó: a=60; b=80; c=100

gọi x;y;z lần lượt là số cây 3 lớp 7A;7B;7C
theo đề ta có: \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)và x+y+z=180
áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{3+4+5}=\frac{180}{12}=15\)
suy ra: \(\frac{x}{3}=15\Rightarrow x=3.15=45\)
\(\frac{y}{4}=15\Rightarrow y=4.15=60\)
\(\frac{z}{5}=15\Rightarrow z=15.5=75\)
vậy số cây 3 lớp 7A;7B;7C lần lượt là : 45;60;75

Gọi `3` lớp `7A,7B,7C` trồng cây lần lượt là `a,b,c` \(\left(a,b,c\in N\right)\)
Theo bài ra ta có : \(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\) và `a+b+c=60`
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{60}{12}=5\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{3}=5\Rightarrow a=5\cdot3=15\\\dfrac{b}{4}=5\Rightarrow b=5\cdot4=20\\\dfrac{c}{5}=5\Rightarrow c=5\cdot5=25\end{matrix}\right.\)
Vậy ...
Gọi \(x;y;z\left(x;y;z>0\right)\) lần lượt là số cây lớp 7A; 7B; 7C trồng
Theo đề bài ta có :
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y+z}{3+4+5}=\dfrac{60}{12}=5\)
\(\Rightarrow\left\{{}\begin{matrix}x=3.5=15\\y=4.5=20\\z=5.5=25\end{matrix}\right.\)
Vậy lớp 7A trồng được : 15 cây
7B trồng được : 20 cây
7C trồng được : 25 cây

Gọi số cây lớp 7a trồng là a; lớp 7b trồng là b, lớp 7c trồng là c
Vì số cây trồng của các lớp đó theo thứ tự tỉ kệ với 3;4;5 nên \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)
Áp dụng tính chất của dãy tỉ sso bằng nhau, ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{180}{12}=15\)
\(\cdot\frac{a}{3}=15\Rightarrow a=45\)
\(\cdot\frac{b}{4}=15\Rightarrow b=60\)
\(\Rightarrow c=180-45-60=75\)
gọi số cây trồng đc của 3 lớp 7A 7B 7C lần lượt là x,y ,z
Theo bài ra ta có :x/3 y/4 z/5 và x+y+z=180
Áp dụng tính chất của dãy tỉ số bằng nhau ta có
x/3 =y/4=z/5=x+y+z/3+4+5=180/12=15
suy ra x/3=15x3=45
y/4=15x4=60
z/5=15x5=75
Vậy số cây lớp 7A trồng đc là 45
số cây lớp 7B trồng đc là 60
số cây lớp 7C trồng đc là 75

Giải:
Gọi số cây lớp 7a,7b,7c trồng được lần lượt là a,b,c (a,b,c\(\in\)N)
Theo bài ra ta có: \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)và a+b+c=180
Theo tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{180}{12}=15\)
+) \(\frac{a}{3}=15\Rightarrow a=45\)
+) \(\frac{b}{4}=15\Rightarrow b=60\)
+) \(\frac{c}{5}=15\Rightarrow c=75\)
Vậy lớp 7a trồng được 45 cây
lớp 7b trồng được 60 cây
lớp 7c trồng được 75 cây

Gọi số cây trồng được của 3 lớp 7A ; 7B ; 7C lần lượt là x,y,z (x,y,z \(\inℕ^∗\))
Theo bài ra ta có :
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}\)và \(2x-y=8\)
=> \(\frac{2x}{4}=\frac{y}{3}=\frac{z}{5}\)
Áp dụng tính chất của dãy tỉ số bằng nhau có:
\(\frac{2x}{4}=\frac{y}{3}=\frac{z}{5}=\frac{2x-y}{2.2-3}=\frac{8}{1}=8\)
=> x = 8 . 2 =16
y = 8 . 3 = 24
z = 8 . 5 = 40
Vậy............................................
Học tốt

gọi số cây 3 lớp 7a. 7b, 7c trồng được lần lượt là : a; b; c (a; b; c thuộc N*; cây)
số cây của 3 lớp 7a; 7b; 7c lần lượt tỉ lệ với 3; 4; 5
=> a/3 = b/4 = c/5
=> (a+b+c)/(4+5+6) = a/3 = b/4 = c/5
mà 3 lớp trồng đươc 180 cây => a + b + c = 180
=> 180/15 = a/3 = b/4 = c/5
=> 16 = a/3 = b/4 = c/5
=> a = 16.3 = 48
b = 16.4= 64
c = 16.5 = 80
Gọi số cây trồng của lớp 7A,7B,7C lần lượt là x,y,z ( x,y,z \(\in\)N* ; x,y,z < 180 )
Theo đề bài ta có : x : y : z = 3 : 4 : 5 hay \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)hay x + y + z = 180
Theo tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{3+4+5}=\frac{180}{12}=15\)
=> \(\hept{\begin{cases}\frac{x}{3}=15\\\frac{y}{4}=15\\\frac{z}{5}=15\end{cases}}\)=> \(\hept{\begin{cases}x=45\\y=60\\z=75\end{cases}}\)
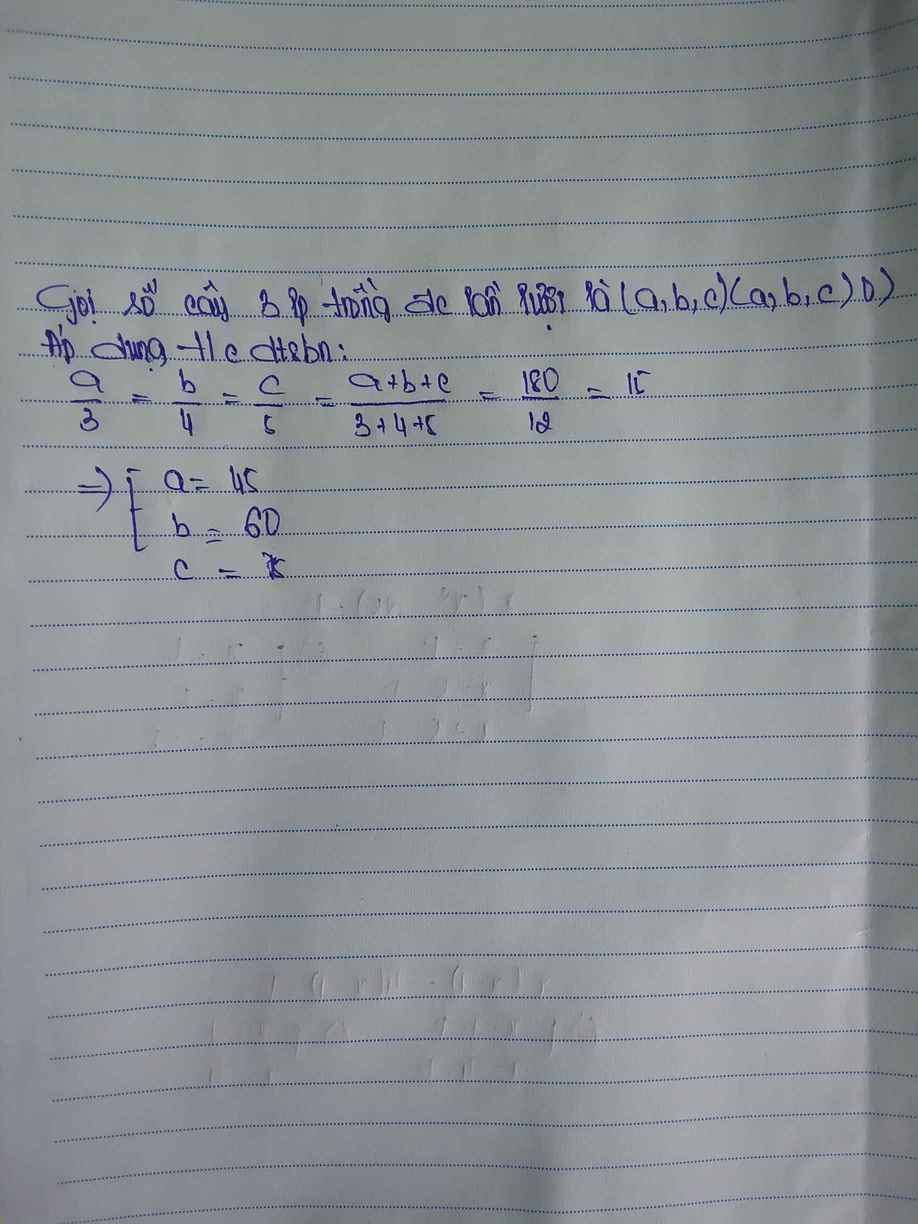
* Gọi số cây trồng được của ba lớp 7A, 7B, 7C lần lượt là a(cây), b(cây) và c(cây)
* Theo đề bài, ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)
a + b + c = 180
* Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{180}{12}=15\)
\(\frac{a}{3}\) = 15 nên a = 15 . 3 = 45
\(\frac{b}{4}\) = 15 nên b = 15 . 4 = 60
\(\frac{c}{5}\) = 15 nên c = 15 . 5 = 75
Vậy số cây trồng được của ba lớp 7A, 7B, 7C lần lượt là 45(cây), 60(cây) và 75(cây)
Cho mik ít đúng nha mấy bạn!!!
Gọi 3 lớp 7A,7B,7C lần lượt là a,b,c (a,b,c thuộc N*).
\(\frac{a}{3}\)=\(\frac{b}{4}\)=\(\frac{c}{5}\) và a + b + c = 180.
Áp dụng tính chất dãy tỉ số bằng nhau.
\(\frac{a}{3}\)= \(\frac{b}{4}\)=\(\frac{c}{5}\) = \(\frac{a+b+c}{3+4+5}\)=\(\frac{180}{12}\)= 15
\(\Leftrightarrow\) \(\frac{a}{3}\)= 15\(\Rightarrow\)a=15\(\times\)3=45
\(\frac{b}{4}\)=15\(\Rightarrow\)b=15\(\times\)4=60
\(\frac{c}{5}\)=15\(\Rightarrow\)c=15\(\times\)5=75
Vậy lớp 7A=45 học sinh
7B=60 học sinh
7C=75 học sinh.