Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số vốn của 3 đơn vị lần lượt là a,b,c
Ta có : a : b : c = 3 : 5 : 7
\(\Rightarrow\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\Rightarrow\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c}{3+5+7}=\dfrac{450}{15}=30\)
\(\Rightarrow a=30.3=90\)
\(b=30.5=150\)
\(c=30.7=210\)
Vậy số tiền lãi lần lượt của 3 đơn vị là 90 triệu , 150 triệu và 210 triệu ( đồng )

Gọi số lãi theo thứ tự là \(a,b,c(a,b,c\in \mathbb{N^*};\text{triệu})\)
Áp dụng tc dtsbn:
\(\dfrac{a}{30}=\dfrac{b}{50}=\dfrac{c}{60}=\dfrac{a+b+c}{30+50+60}=\dfrac{280}{140}=2\\ \Rightarrow\left\{{}\begin{matrix}a=60\\b=100\\c=120\end{matrix}\right.\)
Vậy ...

Bạn Click vô để tham khảo nhé:
Câu hỏi của Ho Pham Phu An - Toán lớp 7 - Học toán với OnlineMath

Gọi số tiền vốn lần lượt là a,b,c(đồng)
Đk:a,b,c<450
a,b,c thuộc N*
Theo bài ra, ta có:
a/3=b/5=c/7 và a+b+c=450
Theo tính chất dãy tỉ số bằng nhau, ta có:
a/3=b/5=c/7=a+b+c/3+5+7=450/15=30
Với:
a/3=30=>a=3.30=90
b/5=30=>b=5.30=150
c/7=30=>c=7.30=210

Gọi a,b,c (triệu đồng) lần lượt là số tiền lãi của 3 đơn vị (0 < a, b, c < 450).
Tổng số tiền lãi là 450 triệu đồng nên a+b+c = 450
Vì số tiền lãi tỉ lệ thuận với số vốn đã góp nên ta có:
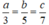
Theo tính chất của dãy tỉ số bằng nhau ta có:
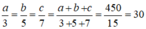
a/3 = 30 ⇒ a = 3.30 = 90
b/5 = 30 ⇒ b = 5.30 = 150
c/7 = 30 ⇒ c = 7.30 = 210
Vậy số tiền lãi được chia cho các đơn vị theo thứ tự là 90 triệu; 150 triệu và 210 triệu

Gọi số tiền lãi mà ba đơn vị được chia là x, y, z
Theo đề bài ta có:
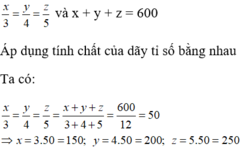
Chọn đáp án D

theo bai ra , ta co : x/2=y/3=z/5 va x+y+z = 135 trieu
ap dung t/c cua day ti so bang nhau , ta co :x+y+z/2+3+5=135/10=13,5
Do do:
x/2 =13,5 nhan 2 = 27
y/3=13,5 nhan 3 = 40,5
z/5=13,5 nhan 5 = 67,5
Vay : Dv 1: 27 trieu
Dv 2 : 40,5 trieu
Dv 3 : 67,5 trieu

Gọi số vốn 3 đơn vị kinh doanh đó lần lượt là a ; b và c tỉ lệ lần lượt với 2 ; 3 và 5
Theo bài ra , ta có :
a + b + c = 350 000 000
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{5}=\frac{a+b+c}{2+3+5}=\frac{350000000}{10}=35000000\)
\(\Rightarrow\hept{\begin{cases}a=35000000.2=70000000\\b=35000000.3=105000000\\c=35000000.5=175000000\end{cases}}\)
Gọi số tiền lãi mỗi đội được chia theo tứ tự từ bé đến lớn lần lượt là:
\(x;y;z\) (triệu đồng); điều kiện \(x;y;z\) > 0
Theo bài ra ta có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y+z}{3+4+5}\) = \(\dfrac{280}{12}\) = \(\dfrac{70}{3}\)
\(x\) = \(\dfrac{70}{3}.3=70\)
y = \(\dfrac{70}{3}.4=\dfrac{280}{3}\)
z = \(\dfrac{70}{3}\).5 = \(\dfrac{350}{3}\)
Kết luận:..