Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Gọi công sai là $d$. Nếu \(-2,x,6,y\) là một cấp số cộng thì:
\(\left\{\begin{matrix} x=-2+d(1)\\ 6=x+d(2)\\ y=6+d(3)\end{matrix}\right.\)
Từ \((1);(2)\Rightarrow 6=x+d=-2+2d\Rightarrow d=4\)
\((1)\Rightarrow x=-2+4=2\)
\((3)\Rightarrow y=6+4=10\)
Do đó đáp án D

Do tam giác đó là tam giác vuông nên có một góc bằng \({90^ \circ }\).
Giả sử hai góc còn lại của tam giác có số đo lần lượt là \(a,b\left( {{0^ \circ } < a,b < {{90}^ \circ }} \right)\).
Vì tổng ba góc trong tam giác bằng \({180^ \circ }\) nên ta có: \(a + b + {90^ \circ } = {180^ \circ } \Leftrightarrow a + b = {90^ \circ }\)(1).
Vì số đo ba góc trong tam giác lập thành cấp số cộng nên ta có:
\(b = \frac{{a + {{90}^ \circ }}}{2} \Leftrightarrow 2b = a + {90^ \circ } \Leftrightarrow - a + 2b = {90^ \circ }\) (2)
Từ (1) và (2) ta có hệ phương trình sau:
\(\left\{ \begin{array}{l}a + b = {90^ \circ }\\ - a + 2b = {90^ \circ }\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = {30^ \circ }\\b = {60^ \circ }\end{array} \right.\)
Vậy số đo ba góc của tam giác vuông đó lần lượt là: \({30^ \circ };{60^ \circ };{90^ \circ }\).

Gọi 3 góc lần lượt là \(a;b;90\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=90\\2b=a+90\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=30\\b=60\end{matrix}\right.\)
Vậy số đo 3 góc là \(30^0;60^0;90^0\)

Chọn C
Ba cạnh a, b, c ( a < b < c) của một tam giác theo thứ tự đó lập thành một cấp số cộng thỏa mãn yêu cầu thì:
a 2 + b 2 = c 2 a + b + c = 3 a + c = 2 b ⇔ a 2 + b 2 = c 2 3 b = 3 a + c = 2 b ⇔ a 2 + b 2 = c 2 b = 1 a = 2 b − c = 2 − c .
Ta có
a 2 + b 2 = c 2 → a = 2 − c b = 1 2 − c 2 + 1 = c 2
⇔ − 4 c + 5 = 0 ⇔ c = 5 4 ⇒ a = 3 4 b = 1 c = 5 4 .

Lời giải:
Vì $a< b< c$ và lập thành 1 csc nên đặt $b=a+d, c=a+2d$.
Theo công thư tính diện tích:
$S=\frac{abc}{4R}=pr$
$\Rightarrow 6Rr=\frac{3abc}{2p}=\frac{3abc}{a+b+c}$
$=\frac{3abc}{a+a+d+a+2d}=\frac{3abc}{3(a+d)}=\frac{3abc}{3b}=ac$ (đpcm)

Chọn C.
Gọi x, y, z theo thứ tự tăng dần của độ dài ba cạnh của tam giác.
Chu vi của tam giác: x + y + z = 3a (1)
Tính chất của cấp số cộng có x + z = 2y (2)
Vì tam giác vuông nên có: x2 + y2 = z2 (3)
Thay (2) vào (1) được 3y = 3a hay y = a, thay y = a vào (2) được: x + z = 2a hay x = 2a - z
Thay x và y vào (3) được: (2a – z)2 + a2 = z2 ⇔ 5a2 – 4az = 0 ⇔ 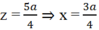
Độ dài ba cạnh của tam giác thỏa yêu cầu: 
Vậy độ dài cạnh lớn nhất của tam giác là ![]()

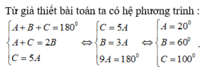
1D
2C