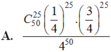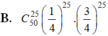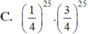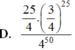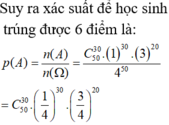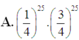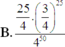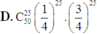Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(sinx-\sqrt{3}cosx=2\left(\dfrac{1}{2}sinx-\dfrac{\sqrt{3}}{2}cosx\right)=2sin\left(x-\dfrac{\pi}{3}\right)=2sint\)
\(y=\sqrt{4sin^2t-4sint-m+3}\)
Hàm xác định trên R khi và chỉ khi:
\(4sin^2t-4sint-m+3\ge0\) ;\(\forall m\)
\(\Leftrightarrow m\le\min\limits_R\left(4sin^2t-4sint+3\right)\)
Ta có: \(4sin^2t-4sint+3=\left(2sint-1\right)^2+2\ge2\)
\(\Rightarrow m\le2\Rightarrow\) có 2 giá trị nguyên dương của m thỏa mãn
20.
Ngôn ngữ đề bài không rõ ràng, có "2 chữ cái giống nhau" ở đây nghĩa là "ít nhất 2 chữ cái giống nhau" hay "cả 2 cặp chữ cái giống nhau" đều đứng cạnh nhau
Không gian mẫu: \(\dfrac{6!}{2!.2!}=180\)
- Theo cách hiểu thứ 2:
Xếp 2 cặp chữ cái: 1 cách
Hoán vị 2 cặp này và 2 chữ còn lại: \(4!=24\) cách
Xác suất: \(P=\dfrac{24}{180}=\dfrac{2}{15}\)
- Theo cách hiểu thứ nhất:
Xếp 2 chữ cái cạnh nhau: 2 cách
Hoán vị 5 chữ cái: \(\dfrac{5!}{2!}=60\) cách
Số cách thỏa mãn: \(2.60-4!=96\)
Xác suất: \(P=\dfrac{96}{180}=\dfrac{8}{15}\)

18C
22D
26B
Giải thích thêm:
ta có: v=s'(t)=3t²-6t+6
a=s"(t)=6t-6
Thời điểm gia tốc bị triệt tiêu khi a=0
⇔6t-6=0
⇔t=1
Vậy v=3.1²-6.1+6=3 (m/s)
32A
34C
35A
cho mình hỏi là tại sao ở câu 26 lại phải đạo hàm thêm lần nữa vậy?

k ở đây được hiểu là "một số nguyên bất kì", giống hay khác nhau đều được
Ví dụ:
\(sinx=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Thì "k" trong \(\dfrac{\pi}{6}+k2\pi\) và "k" trong \(\dfrac{5\pi}{6}+k2\pi\) không liên quan gì đến nhau (nó chỉ là 1 kí hiệu, có thể k trên bằng 0, k dưới bằng 100 cũng được, không ảnh hưởng gì, cũng có thể 2 cái bằng nhau cũng được).
Khi người ta ghi 2 nghiệm đều là "k2pi" chủ yếu do... lười biếng (kiểu như mình). Trên thực tế, rất nhiều tài liệu cũ họ ghi các kí tự khác nhau, ví dụ 1 nghiệm là \(\dfrac{\pi}{6}+k2\pi\), 1 nghiệm là \(\dfrac{5\pi}{6}+n2\pi\) để tránh học sinh phát sinh hiểu nhầm đáng tiếc rằng "2 cái k phải giống hệt nhau về giá trị".

Đáp án B
Học sinh đó làm đúng được 5 điểm khi làm được đúng 25 câu bất kỳ trong số 50 câu, 25 câu còn lại làm sai.
Xác suất để học sinh là đúng một câu bất kỳ là 1 4 , làm sai một câu là . Do đó xác suất để học sinh đó làm đúng 25 câu bất kỳ trong số 50 câu là C 50 25 . 1 4 25 .
Xác suất để hoạc sinh đó làm sai 25 câu còn lại là 3 4 25 .
Vậy xác suất để học sinh đó làm được đúng 5 điểm là: C 50 25 . 1 4 25 . 3 4 25

Đáp án D
Học sinh đó làm đúng được 5 điểm khi làm được đúng 25 câu bất kỳ trong số 50 câu, 25 câu còn lại làm sai.
Xác suất để học sinh là đúng một câu bất kỳ là 1 4 , làm sai một câu là 3 4 . Do đó xác suất để học sinh đó làm đúng 25 câu bất kỳ trong số 50 câu là C 50 25 . 1 4 25 .
Xác suất để hoạc sinh đó làm sai 25 câu còn lại là 3 4 25 .
Vậy xác suất để học sinh đó làm được đúng 5 điểm là: C 50 25 . 1 4 25 . 3 4 25

Tổng cộng có \(4^{10}\) khả năng xảy ra
Trong đó có đúng 1 khả năng được 10 điểm
Do đó có \(4^{10}-1\) phương án trả lời ko được 10 điểm

Gọi x là số câu trả lời đúng \(\Rightarrow50-x\) câu trả lời sai
Số điểm đạt được:
\(0,2.x-0,05\left(50-x\right)=4,5\)
\(\Rightarrow x=28\)
Vậy học sinh đó trả lời đúng 28 câu và trả lời sai 22 câu
Có \(C_{50}^{28}\) cách chọn 28 câu từ 50 câu
Ở mỗi câu, học sinh có \(\dfrac{1}{4}\) xác suất trả lời đúng và \(\dfrac{3}{4}\) xác suất trả lời sai
Do đó, xác suất học sinh đó được 4,5 điểm là:
\(C_{50}^{28}.\left(\dfrac{1}{4}\right)^{28}.\left(\dfrac{3}{4}\right)^{22}=...\)