Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có :
\(S=\dfrac{1}{5}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\)
\(S=\dfrac{1}{5}+\left(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}\right)+\left(\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\right)\)
Nhận xét :
\(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}< \dfrac{1}{12}+\dfrac{1}{12}+\dfrac{1}{12}=\dfrac{1}{4}\)
\(\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}< \dfrac{1}{60}+\dfrac{1}{60}+\dfrac{1}{60}=\dfrac{1}{20}\)
\(\Rightarrow S< \dfrac{1}{5}+\dfrac{1}{4}+\dfrac{1}{20}\)
\(\Rightarrow S< \dfrac{1}{2}\rightarrowđpcm\)
Giải:
Ta có:
\(S=\dfrac{1}{5}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\)
\(=\dfrac{1}{5}+\left(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}\right)+\) \(\left(\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\right)\)
Nhận xét:
\(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}< \dfrac{1}{12}+\dfrac{1}{12}+\dfrac{1}{12}=\dfrac{1}{4}\)
\(\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}< \dfrac{1}{60}+\dfrac{1}{60}+\dfrac{1}{60}=\dfrac{1}{20}\)
\(\Rightarrow S< \dfrac{1}{5}+\dfrac{1}{4}+\dfrac{1}{20}=\dfrac{1}{2}\)
Vậy \(S=\dfrac{1}{5}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\) \(< \dfrac{1}{2}\) (Đpcm)
\(\dfrac{1}{5}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}< \dfrac{1}{5}+\dfrac{1}{13}\cdot3+\dfrac{1}{61}\cdot3\\ =\dfrac{1}{5}+\dfrac{3}{13}+\dfrac{3}{61}< \dfrac{1}{5}+\dfrac{3}{12}+\dfrac{3}{60}=\dfrac{1}{5}+\dfrac{1}{4}+\dfrac{1}{20}=\dfrac{1}{2}\)
=> Điều phải chứng minh
Giải:
Ta có: \(S=\dfrac{1}{5}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\)
\(=\dfrac{1}{5}+\left(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}\right)\) \(+\left(\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\right)\)
Dễ thấy:
\(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}< \dfrac{1}{12}+\dfrac{1}{12}+\dfrac{1}{12}=\dfrac{1}{4}\)
\(\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}< \dfrac{1}{60}+\dfrac{1}{60}+\dfrac{1}{60}=\dfrac{1}{20}\)
\(\Rightarrow S< \dfrac{1}{5}+\dfrac{1}{4}+\dfrac{1}{20}=\dfrac{1}{2}\)
Vậy \(S< \dfrac{1}{2}\) (Đpcm)
Lời giải:
Ta có:
\(\left\{\begin{matrix} \frac{1}{13}< \frac{1}{12}\\ \frac{1}{14}< \frac{1}{12}\\ \frac{1}{15}< \frac{1}{12}\end{matrix}\right.\Rightarrow \frac{1}{13}+\frac{1}{14}+\frac{1}{15}< \frac{3}{12}=\frac{1}{4}(1)\)
\(\left\{\begin{matrix} \frac{1}{61}< \frac{1}{60}\\ \frac{1}{62}< \frac{1}{60}\\ \frac{1}{63}< \frac{1}{60}\end{matrix}\right.\Rightarrow \frac{1}{61}+\frac{1}{62}+\frac{1}{63}< \frac{3}{60}=\frac{1}{20}(2)\)
Từ \((1);(2)\Rightarrow \frac{1}{5}+\frac{1}{13}+\frac{1}{14}+\frac{1}{15}+\frac{1}{61}+\frac{1}{62}+\frac{1}{63}< \frac{1}{5}+\frac{1}{4}+\frac{1}{20}\)
Hay \( \frac{1}{5}+\frac{1}{13}+\frac{1}{14}+\frac{1}{15}+\frac{1}{61}+\frac{1}{62}+\frac{1}{63}< \frac{1}{2}\)
Ta có đpcm.
Đặt A là biểu thức đó
Ta có:
\(\dfrac{1}{13}< \dfrac{1}{12};\dfrac{1}{14}< \dfrac{1}{12};\dfrac{1}{15}< \dfrac{1}{12}\)
\(\Rightarrow\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}< \dfrac{1}{12}\)
Ta cũng có
\(\dfrac{1}{61}< \dfrac{1}{60};\dfrac{1}{62}< \dfrac{1}{60};\dfrac{1}{63}< \dfrac{1}{60}\)
\(\Rightarrow\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}< \dfrac{1}{60}\)
\(\Rightarrow A< \dfrac{1}{5}+\dfrac{1}{12}.3+\dfrac{1}{60}.3\)
\(\Rightarrow A< \dfrac{1}{5}+\dfrac{1}{4}+\dfrac{1}{20}=\dfrac{1}{2}\)
\(\Rightarrow\)dpcm
Sai đề rồi \(\dfrac{1}{13}\) chứ đâu phải \(\dfrac{1}{3}\)
Ta có: \(S=\dfrac{1}{5}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\)
\(S=\dfrac{1}{5}+\left(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}\right)+\left(\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\right)\)
\(< \dfrac{1}{5}+\left(\dfrac{1}{13}+\dfrac{1}{13}+\dfrac{1}{13}\right)+\left(\dfrac{1}{61}+\dfrac{1}{61}+\dfrac{1}{61}\right)\)
\(=\dfrac{1}{5}+\dfrac{1}{13}.3+\dfrac{1}{61}.3\)
\(=\dfrac{1}{5}+\dfrac{3}{13}+\dfrac{3}{61}\)
\(< \dfrac{1}{5}+\dfrac{3}{12}+\dfrac{3}{60}\)
\(=\dfrac{1}{5}+\dfrac{1}{4}+\dfrac{1}{20}\)
\(=\dfrac{10}{20}\)\(=\dfrac{1}{2}\)
Vậy S\(< \dfrac{1}{2}\) (đpcm)
2 hàng cuối có vấn đề \(\dfrac{10}{20}=\dfrac{1}{2}\) rồi mà, sao còn bé hơn, vô lí
Giải
Ta có : \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};\dfrac{1}{4^2}< \dfrac{1}{3.4};...;\dfrac{1}{20^2}< \dfrac{1}{19.20}\)
\(\Rightarrow\)D < \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{19.20}\)
Nhận xét: \(\dfrac{1}{1.2}=1-\dfrac{1}{2};\dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3};\dfrac{1}{3.4}=\dfrac{1}{3}-\dfrac{1}{4};...;\dfrac{1}{19.20}=\dfrac{1}{19}-\dfrac{1}{20}\)
\(\Rightarrow\) D< 1- \(\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{19}-\dfrac{1}{20}\)
D< 1 - \(\dfrac{1}{20}\)
D< \(\dfrac{19}{20}\)<1
\(\Rightarrow\)D< 1
Vậy D=\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{5^2}\)<1
A=\(\dfrac{1}{2^2}+\dfrac{1}{4^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}\)
A=\(\dfrac{1}{2^2.1}+\dfrac{1}{2^2.2^2}+\dfrac{1}{3^2.2^2}+...+\dfrac{1}{50^2.2^2}\)
A=\(\dfrac{1}{2^2}\left(1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{50^2}\right)\)
\(A=\dfrac{1}{2^2}\left(1+\dfrac{1}{2.2}+\dfrac{1}{3.3}+...+\dfrac{1}{50.50}\right)\)
Ta có :
\(\dfrac{1}{2.2}< \dfrac{1}{1.2};\dfrac{1}{3.3}< \dfrac{1}{2.3};\dfrac{1}{4.4}< \dfrac{1}{3.4};...;\dfrac{1}{50.50}< \dfrac{1}{49.50}\)
\(\Rightarrow A< \dfrac{1}{2^2}\left(1+\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{49.50}\right)\)Nhận xét :
\(\dfrac{1}{1.2}< 1-\dfrac{1}{2};\dfrac{1}{2.3}< \dfrac{1}{2}-\dfrac{1}{3};...;\dfrac{1}{49.50}< \dfrac{1}{49}-\dfrac{1}{50}\)
\(\Rightarrow A< \dfrac{1}{2^2}\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{49}-\dfrac{1}{50}\right)\)
A<\(\dfrac{1}{2^2}\left(1-\dfrac{1}{50}\right)\)
A<\(\dfrac{1}{4}.\dfrac{49}{50}\)<1
A<\(\dfrac{49}{200}< \dfrac{1}{2}\)
\(\Rightarrow A< \dfrac{1}{2}\)
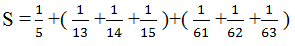
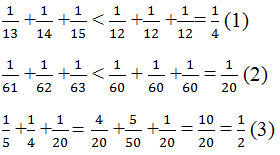
a) Giải:
Ta có: \(4n-5=4\left(n-3\right)+7\)
Để \(\left(4n-5\right)⋮\left(n-3\right)\Leftrightarrow7⋮n-3\)
\(\Rightarrow n-3\inƯ\left(7\right)\)
Mà \(Ư\left(7\right)\in\left\{\pm1;\pm7\right\}\)
Nên ta có bảng sau:
Vậy \(n=\left\{2;4;-4;10\right\}\)
b) Ta có:
\(S=\dfrac{1}{5}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\)
\(=\dfrac{1}{5}+\left(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}\right)+\left(\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\right)\)
Nhận xét:
\(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}< \dfrac{1}{12}+\dfrac{1}{12}+\dfrac{1}{12}=\dfrac{1}{4}\)
\(\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}< \dfrac{1}{60}+\dfrac{1}{60}+\dfrac{1}{60}=\dfrac{1}{20}\)
\(\Rightarrow S< \dfrac{1}{5}+\dfrac{1}{4}+\dfrac{1}{20}=\dfrac{1}{2}\)
Vậy \(S=\dfrac{1}{5}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\) \(< \dfrac{1}{2}\) (Đpcm)