Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

The first side of the square known as a ; 2nd side of the square is b \(\left(a>b\right)\)
\(\Rightarrow a^2+b^2=100\)
\(\Rightarrow a^2+b^2=36+64\)
\(\Rightarrow\begin{cases}a=8\\b=4\end{cases}\)
=> The perimeter = \(8.3+3.6+8-6=24+18-2=40\left(cm\right)\)

2. A B C D O E F
+ AB // CD \(\Rightarrow\dfrac{AO}{CO}=\dfrac{BO}{DO}\)
\(\Rightarrow\dfrac{AO}{AO+CO}=\dfrac{BO}{BO+DO}\Rightarrow\dfrac{AO}{AC}=\dfrac{BO}{BD}\)
+ OE // CD => \(\dfrac{OE}{CD}=\dfrac{AO}{AC}\)
+ OF // CD => \(\dfrac{OF}{DC}=\dfrac{BO}{BD}\)
\(\Rightarrow\dfrac{OE}{CD}=\dfrac{OF}{DC}\Rightarrow OE=OF\)
Bài 1:
a: Xét hình thang ABCD có MN//AB//CD
nên AM/MD=BN/NC
b: AM/MD=BN/NC
=>MD/AM=NC/BN
=>\(\dfrac{MD+AM}{AM}=\dfrac{NC+BN}{BN}\)
=>AD/AM=BC/BN
=>AM/AD=BN/BC
c: AM/AD=BN/BC
=>1-AM/AD=1-BN/BC
=>DM/AD=CN/CB

a: Gọi K là trung điểm của NC
=>AN=NK=KC
Xét ΔBNC có
M,K lần lượt là trung điểm của CB và CN
nên MK là đường trung bình
=>MK//BN và MK=1/2BN
Xét ΔAMK có
N là trung điểm của AK
NI//MK
Do đó: I là trung điểm của AM
b: Xét ΔAMK có IN//MK
nên IN/MK=AN/AK=1/2
=>IN=1/2MK=1/2x1/2BN=1/4BN
=>IN=1/3BI
c: Gọi D là trung điểm của BE
=>AE=ED=BD
Xét ΔBEC có
M,D lần lượt là trung điểm của BC,BE
nên MD là đường trung bình
=>MD//EC
Xét ΔADM cso
I,E lần lượt là trung điểm của AM và AD
nen IE là đường trung bình
=>IE//MD
=>IE//EC
=>C,I,E thẳng hàng
a: Gọi K là trung điểm của NC
=>AN=NK=KC
Xét ΔBNC có
M,K lần lượt là trung điểm của CB và CN
nên MK là đường trung bình
=>MK//BN và MK=1/2BN
Xét ΔAMK có
N là trung điểm của AK
NI//MK
Do đó: I là trung điểm của AM
b: Xét ΔAMK có IN//MK
nên IN/MK=AN/AK=1/2
=>IN=1/2MK=1/2x1/2BN=1/4BN
=>IN=1/3BI
c: Gọi D là trung điểm của BE
=>AE=ED=BD
Xét ΔBEC có
M,D lần lượt là trung điểm của BC,BE
nên MD là đường trung bình
=>MD//EC
Xét ΔADM cso
I,E lần lượt là trung điểm của AM và AD
nen IE là đường trung bình
=>IE//MD
=>IE//EC
=>C,I,E thẳng hàng

Kẽ EG vuông góc BC=> AF=BG=5cm
=>GC=BC-BG=9-5=4cm
\(S_{ABCDEF}=S_{ABGF}+S_{EGCD}=5.6+4.4=46cm^2\)


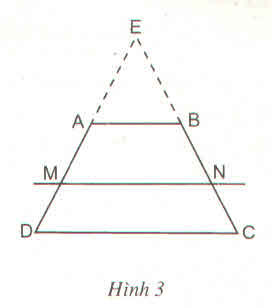




kẻ AC cắt MN tại I
ta có \(\dfrac{AM}{MD}=\dfrac{BN}{NC}\left(=\dfrac{1}{2}\right)\Rightarrow\)MN//DC//AB(định lí Talet đảo)
ta có:
\(\dfrac{AM}{MD}=\dfrac{1}{2}\Rightarrow\dfrac{AM}{AD}=\dfrac{AM}{AM+MD}=\dfrac{1}{1+2}=\dfrac{1}{3}\\ \Rightarrow\dfrac{BN}{BC}=\dfrac{1}{3}\Rightarrow\dfrac{NC}{BC}=\dfrac{2}{3}\)
tam giác ADC có MI//DC nên :\(\dfrac{MI}{DC}=\dfrac{AM}{AD}\Rightarrow\dfrac{MI}{\left(x+2\right)\left(x-2\right)}=\dfrac{1}{3}\Rightarrow\left(x+2\right)\left(x-2\right)=3MI\)
tam giac CAB có IN//AB nên:
\(\dfrac{NI}{AB}=\dfrac{BN}{BC}\Rightarrow\dfrac{NI}{x+4}=\dfrac{2}{3}\Rightarrow2\left(x+4\right)=3NI\)
\(\left(x+2\right)\left(x-2\right)+2\left(x+4\right)=3MI+3NI\\ \Leftrightarrow x^2-4+2x+8=3\left(MI+NI\right)=3MN=39\\ \Leftrightarrow x^2+2x+4-39=0\\ \Leftrightarrow x^2+2x-35=0\\ \Leftrightarrow\left(x-5\right)\left(x+7\right)=0\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-7\end{matrix}\right.\)
Vậy x=5 hoặc x=-7