Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta sắp xếp dãy số áo bán được theo dãy tăng dần:
36, 36, 36, …, 36, 37, 37, …, 37, 38, 38, …, 38, …., 42, 42.
Dãy số gồm 465 số nên số trung vị là số đứng ở vị trí thứ 233.
Số thứ 233 là số 39.
Vậy Me = 39.

a)
Bảng tần số:
Cỡ giày | 38 | 39 | 40 | 41 |
Số giày | 3 | 9 | 2 | 1 |
Cỡ giày trung bình:
\(\bar X = \frac{{38.3 + 39.9 + 40.2 + 41}}{{3 + 9 + 2 + 1}} = \frac{{586}}{{15}} \approx 39\)
Ý nghĩa: Cỡ giày trung bình này có thể đại diện cho cỡ giày của cửa hàng.
b) Cỡ giày số 39 là cỡ giày nhiều khách nam đi nhất trong tổng số người được chọn nên cửa hàng nên nhập cỡ giày này.

Gọi x, y, z (đồng) lần lượt là giá tiền mỗi áo, quần và váy (0 < x, y, z < 5259000).
Ngày thứ nhất bán được 21 áo, 21 quần và 18 váy, doanh thu là 5.349.000 đồng nên ta có:
12x + 21y + 18z = 5.349.000
Ngày thứ hai bán được 16 áo, 24 quần và 12 váy, doanh thu là 5.600.000 đồng nên ta có:
16x + 24y + 12z = 5.600.000
Ngày thứ ba bán được 24 áo, 15 quần và 12 váy, doanh thu là 5.259.000 đồng nên ta có:
24x + 15y + 12z = 5.259.000
Từ đó ta có hệ phương trình:
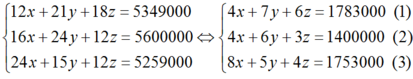
Lấy (1) – (2) ta được : y + 3z = 383000.
Nhân 2 vào hai vế của (1) rồi trừ đi (3) ta được: 9y + 8z = 1813000
Ta có hệ phương trình:
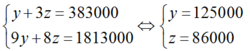
Thay y = 125000, z = 86000 vào (1) ta được x = 98000.
Vậy: Giá bán mỗi áo là: 98.000 đồng.
Giá bán mỗi quần là: 125.000 đồng.
Giá bán mỗi váy là: 86.000 đồng.

Cỡ áo mà cửa hàng bác Tâm bán được nhiều nhất trong tháng đầu tiên là cỡ áo: 40 (số áo bán được là 81).

Như hpt lớp 8.
Gọi giá bán áo là x , giá bán quần là y, giá bán váy là z.
Theo đề bài ta có :
\(\left\{{}\begin{matrix}12x+21y+18z=5349000\\16x+24y+12z=5600000\\24x+15y+12z=5259000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=98000\\y=125000\\z=86000\end{matrix}\right.\)
Vậy giá bán áo là 98000 đồng, giá bán quần là 125000 đồng, giá bán váy là 86000 đồng.
Gọi giá tiền mỗi cái áo là \(x\) (đồng), giá tiền mỗi cái quần là \(y\) (đồng), giá tiền mỗi cái váy là \(z\) (đồng)
ĐK : \(x,y,z\in N^{\circledast}\)
Vì ngày thứ nhất bán được 12 áo, 21 quần và 18 váy, doanh thu 5 349 000 đồng nên
ta có phương trình : \(12x+21y+18z=5349000\) (1)
Vì ngày thứ hai bán được 16 áo, 24 quần và 12 váy, doanh thu 5 600 000 đồng nên
ta có phương trình : \(16x+24y+12z=5600000\) (2)
Vì ngày thứ ba bán được 24 áo, 15 quần và 12 váy, doanh thu 5 259 000 đồng nên
ta có phương trình : \(24x+15y+12z=5259000\) (3)
Từ (1),(2) và (3) ta có hệ phương trình :
\(\left\{{}\begin{matrix}12x+21y+18z=5349000\\16x+24y+12z=5600000\\24x+15y+12z=5259000\end{matrix}\right.\)
Giải hệ phương trình : \(\left\{{}\begin{matrix}12x+21y+18z=5349000\\16x+24y+12z=5600000\\24x+15y+12z=5259000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=98000\left(TM\right)\\y=125000\left(TM\right)\\z=86000\left(TM\right)\end{matrix}\right.\)
Vậy giá tiền mỗi cái áo là 98000 đồng, giá tiền mỗi cái quần là 125000, giá tiền mỗi cái váy là 86000 đồng

a) Năm 2019:
+) Số trung bình: \(\overline x = \frac{{54 + 22 + 24 + 30 + 35 + 40 + 31 + 29 + 29 + 37 + 40 + 31}}{{12}} = 33,5\)
+) Phương sai \({S^2} = \frac{1}{{12}}\left( {{{54}^2} + {{22}^2} + ... + {{31}^2}} \right) - 33,{5^2} = 67,25\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 8,2\)
+) Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 22, 24, 29, 29, 30, 31, 31, 35, 37, 40, 40, 54
\({Q_2} = {M_e} = \frac{1}{2}(31 + 31) = 31\)
\({Q_1}\) là trung vị của nửa số liệu: 22, 24, 29, 29, 30, 31. Do đó \({Q_1} = 29\)
\({Q_3}\) là trung vị của nửa số liệu: 31, 35, 37, 40, 40, 54. Do đó \({Q_3} = 38,5\)
\( \Rightarrow {\Delta _Q} = 38,5 - 29 = 9,5\)
Năm 2020:
+) Số trung bình: \(\overline x = 34,5\)
+) Phương sai \({S^2} = \frac{1}{{12}}\left( {{{45}^2} + {{28}^2} + ... + {{37}^2}} \right) - 34,{5^2} = 15,75\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 3,97\)
+) Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 28, 31, 32, 33, 33, 34, 34, 35, 35, 37, 37, 45.
\({Q_2} = {M_e} = \frac{1}{2}(34 + 34) = 34\)
\({Q_1}\) là trung vị của nửa số liệu: 28, 31, 32, 33, 33, 34. Do đó \({Q_1} = 32,5\)
\({Q_3}\) là trung vị của nửa số liệu: 34, 35, 35, 37, 37, 45. Do đó \({Q_3} = 36\)
\( \Rightarrow {\Delta _Q} = 36 - 32,5 = 3,5\)
b) Nhận xét:
So sánh số trung bình: số lượng bán ra trung bình theo tháng không tăng nhiều so với năm trước (tăng 1)
So sánh độ lệch chuẩn: Số lượng xe bán ra năm 2020 không có sự chênh lệch quá nhiều giữa các tháng.
=> Tác động của chiến lược: Số lượng xe bán ra tăng ít, nhưng đồng đều giữa các tháng.

Bảng số liệu có 7 giá trị, sắp các giá trị theo thứ tự không giảm ta có:
650, 670, 690, 720, 840, 2500, 3000.
Vì số phần tử = 7 là số lẻ nên số trung vị là Me = 720 (số chính giữa của dãy).
Ý nghĩa:
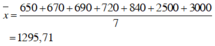
Số trung bình này chênh lệch quá lớn so với các số liệu nên không đại diện được cho các số liệu.
Trong trường hợp này, số trung vị nên được chọn làm giá trị đại diện cho mức lương.

Đáp án B.
Số quần bán được là 379 chiếc
⇒ Số trung vị M e là số chính giữa của dãy khi xếp số quần bán được thành một dãy không giảm
⇒ M e là quần có size đứng ở vị trí 190 ⇒ M e = 27

Để cửa hàng có lãi thì lợi nhuận lớn hơn 0, suy ra \(I > 0 \Leftrightarrow - 3{x^2} + 200x - 2325 > 0\)
Tam thức \(I = - 3{x^2} + 200x - 2325\) có \(\Delta = 12100 > 0\), có hai nghiệm phân biệt \({x_1} = 15;{x_2} = \frac{{155}}{3}\) và có \(a = - 3 < 0\)
Ta có bảng xét dấu như sau:
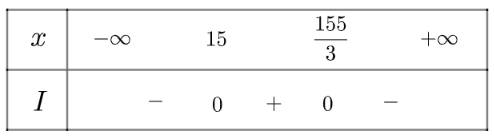
Vậy ta thấy cửa hàng có lợi nhuận khi \(x \in \left( {15;\frac{{155}}{3}} \right)\) (kg)
