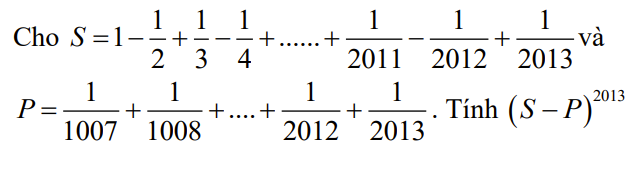Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách giải như sau: đặt số bưu ảnh An có = x + a ; số bưu ảnh Bách có = y + a (trong đó a = số bưu ảnh hoa của An = số bưu ảnh thú rừng của Bách)
Theo đề bài ta lập được hệ pt sau:
x + 2a = 7y
x = 4 (y + 2a)
Giải hệ ta có x = 64a/3 và y = 10a/3 !!
a chỉ có thể là bội số của 3. cho a = 3, hệ có nghiệm x = 64, y = 10, số bưu ảnh An có 67 và số bưu ảnh Bách có 13 (thỏa yêu cầu đề bài)
a = 6 ==> x = 128 > 100 (không thỏa yêu cầu đề bài). Vậy suy ra nhận nghiệm duy nhất a = 3.
Và đáp án chỉ có 1 nghiệm duy nhất. Bưu ảnh An có là 67 và Bách có 13. Trong đó số bưu ảnh hoa của An là 3, số bưu ảnh thú rừng của Bách cũng là 3. Ok ??
Theo đề bài ta lập được hệ pt sau:
x + 2a = 7y
x = 4 (y + 2a)
Giải hệ ta có x = 64a/3 và y = 10a/3 !!
a chỉ có thể là bội số của 3. cho a = 3, hệ có nghiệm x = 64, y = 10, số bưu ảnh An có 67 và số bưu ảnh Bách có 13 (thỏa yêu cầu đề bài)
a = 6 ==> x = 128 > 100 (không thỏa yêu cầu đề bài). Vậy suy ra nhận nghiệm duy nhất a = 3.
Và đáp án chỉ có 1 nghiệm duy nhất. Bưu ảnh An có là 67 và Bách có 13. Trong đó số bưu ảnh hoa của An là 3, số bưu ảnh thú rừng của Bách cũng là 3

Lời giải:
Gọi số bưu ảnh của An và Bách là $a,b(a,b>0)$. Số bưu ảnh hoa của An và số bưu ảnh thú của Bách bằng $c(c>0)$
Theo bài ra ta có:
$a+c=7(b-c)\Rightarrow a+8c=7b(1)$
Và $a-c=4(b+c)\Rightarrow a-5c=4b(2)$
Lấy $(1)-(2)\Rightarrow 13c=3b\Rightarrow c=\frac{3b}{13}$
$\Rightarrow a=5c+4b=5.\frac{3b}{13}+4b=\frac{67b}{13}$
Vì $a< 100$ nên $\frac{67b}{13}< 100\Rightarrow b< 20(*)$
Mặt khác $a$ là số tự nhiên nên $\frac{67b}{13}$ cũng là số tự nhiên, suy ra $b\vdots 13(**)$
Từ $(*); (**)$ kết hợp với $b>0$ suy ra $b=13$
$\Rightarrow a=67$
Vậy An có 67 bưu ảnh, Bách có 13 bưu ảnh.

Câu 1:
\(n^2+3⋮n-1\)
\(\Leftrightarrow n^2-1+4⋮n-1\)
\(\Leftrightarrow4⋮n-1\)
\(\Leftrightarrow n-1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{2;0;3;-1;5;-3\right\}\)

\(P=\dfrac{1}{1007}+\dfrac{1}{1008}+...+\dfrac{1}{2012}+\dfrac{1}{2013}\)
\(=\left(1+\dfrac{1}{2}+...+\dfrac{1}{1006}+\dfrac{1}{1007}+\dfrac{1}{1008}+...+\dfrac{1}{2012}+\dfrac{1}{2013}\right)\)
\(=\left(1+\dfrac{1}{2}+...+\dfrac{1}{1006}\right)\)
\(=\left(1+\dfrac{1}{2}+...+\dfrac{1}{1006}+\dfrac{1}{1007}+\dfrac{1}{1008}+...+\dfrac{1}{2012}+\dfrac{1}{2013}\right)\)
\(=2.\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+...+\dfrac{1}{2012}\right)\)
\(=1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...-\dfrac{1}{2012}+\dfrac{1}{2013}=S\)
Do đó \(\left(S-P\right)^{2013}=0\)