NL
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
8 tháng 8 2018
Bài 1:
Nếu $n$ không chia hết cho $7$ thì:
\(n\equiv 1\pmod 7\Rightarrow n^3\equiv 1^3\equiv 1\pmod 7\Rightarrow n^3-1\vdots 7\)
\(n\equiv 2\pmod 7\Rightarrow n^3\equiv 2^3\equiv 1\pmod 7\Rightarrow n^3-1\vdots 7\)
\(n\equiv 3\pmod 7\Rightarrow n^3\equiv 3^3\equiv -1\pmod 7\Rightarrow n^3+1\vdots 7\)
\(n\equiv 4\equiv -3\pmod 7\Rightarrow n^3\equiv (-3)^3\equiv 1\pmod 7\Rightarrow n^3-1\vdots 7\)
\(n\equiv 5\equiv -2\pmod 7\Rightarrow n^3\equiv (-2)^3\equiv -1\pmod 7\Rightarrow n^3+1\vdots 7\)
\(n\equiv 6\equiv -1\pmod 7\Rightarrow n^3\equiv (-1)^3\equiv -1\pmod 7\Rightarrow n^3+1\vdots 7\)
Vậy \(n^3-1\vdots 7\) hoặc \(n^3+1\vdots 7\)
AH
Akai Haruma
Giáo viên
8 tháng 8 2018
b)
Đặt \(A=mn(m^2-n^2)(m^2+n^2)\)
Nếu $m,n$ có cùng tính chẵn lẻ thì \(m^2-n^2\) chẵn, do đó \(A\vdots 2\)
Nếu $m,n$ không cùng tính chẵn lẻ, có nghĩa trong 2 số $m,n$ tồn tại một số chẵn và một số lẻ, khi đó \(mn\vdots 2\Rightarrow A\vdots 2\)
Tóm lại, $A$ chia hết cho $2$
---------
Nếu trong 2 số $m,n$ có ít nhất một số chia hết cho $3$ thì \(mn\vdots 3\Rightarrow A\vdots 3\)
Nếu cả hai số đều không chia hết cho $3$. Ta biết một tính chất quen thuộc là một số chính phương chia $3$ dư $0$ hoặc $1$. Vì $m,n$ không chia hết cho $3$ nên:
\(m^2\equiv n^2\equiv 1\pmod 3\Rightarrow m^2-n^2\vdots 3\Rightarrow A\vdots 3\)
Vậy \(A\vdots 3\)
-----------------
Nếu tồn tại ít nhất một trong 2 số $m,n$ chia hết cho $5$ thì hiển nhiên $A\vdots 5$
Nếu cả 2 số đều không chia hết cho $5$. Ta biết rằng một số chính phương khi chia $5$ dư $0,1,4$. Vì $m,n\not\vdots 5$ nên \(m^2,n^2\equiv 1,4\pmod 5\)
+Trường hợp \(m^2,n^2\) cùng số dư khi chia cho $5$\(\Rightarrow m^2-n^2\equiv 0\pmod 5\Rightarrow m^2-n^2\vdots 5\Rightarrow A\vdots 5\)
+Trường hợp $m^2,n^2$ không cùng số dư khi chia cho $5$
\(\Rightarrow m^2+n^2\equiv 1+4\equiv 0\pmod 5\Rightarrow m^2+n^2\vdots 5\Rightarrow A\vdots 5\)
Tóm lại $A\vdots 5$
Vậy \(A\vdots (2.3.5)\Leftrightarrow A\vdots 30\) (do $2,3,5$ đôi một nguyên tố cùng nhau)
Ta có đpcm.
24 tháng 5 2022
1: \(\dfrac{A}{B}=\dfrac{4}{3}x^{n+1-3}y^{2-n+1}=\dfrac{4}{3}x^{n-2}y^{3-n}\)
Để A chia hết cho B thì \(\left\{{}\begin{matrix}n-2>=0\\3-n< =0\end{matrix}\right.\Leftrightarrow2< =n< =3\)
2: \(\dfrac{A}{B}=\dfrac{7}{5}x^{n-1-2}y^{5-n}-xy^{4-n}=\dfrac{7}{5}x^{n-3}y^{5-n}-xy^{4-n}\)
Để A chia hết cho B thì \(\left\{{}\begin{matrix}n-3>=0\\5-n>=0\\4-n>=0\end{matrix}\right.\Leftrightarrow3\le n\le4\)
27 tháng 8 2022
b: \(\Leftrightarrow n^3-8+6⋮n-2\)
\(\Leftrightarrow n-2\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
hay \(n\in\left\{3;1;4;0;5;-1;8;-4\right\}\)
c: \(\Leftrightarrow n^3+n^2+n-4n^2-4n-4+3⋮n^2+n+1\)
\(\Leftrightarrow n^2+n+1\in\left\{1;-1;3;-3\right\}\)
\(\Leftrightarrow n^2+n+1\in\left\{1;3\right\}\)
\(\Leftrightarrow\left[{}\begin{matrix}n^2+n=0\\n^2+n-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}n\left(n+1\right)=0\\\left(n+2\right)\left(n-1\right)=0\end{matrix}\right.\Leftrightarrow n\in\left\{0;-1;-2;1\right\}\)
3 tháng 11 2017
a,
6n^2 - n + 5 2n + 1 3n - 2 6n^2 + 3n -4n + 5 -4n - 2 7 \
Để \(A⋮B\) \(\Leftrightarrow7⋮2n+5\) \(\Leftrightarrow2n+5\inƯ\left(7\right)=\left\{1;7;-1;-7\right\}\)
Ta có bảng sau :
| \(2n+5\) | \(1\) | \(7\) | \(-1\) | \(-7\) |
| \(n\) | \(-2\) | \(1\) | \(-3\) | \(-6\) |
Vậy \(\left[{}\begin{matrix}n=-2\\n=1\\n=-3\\n=-6\end{matrix}\right.\) thì A chia hết cho B
b, tường tự câu a
Nếu mà bn ko lm đc thì nói mk ,mk sẽ giải cho
3 tháng 11 2017
Đặt tính chia:
6n-n+5 2 2n+1 3n-2 6n+3n - 2 -4n+5 - -4n-2 _______________ 7
\(\Rightarrow\text{Để }A⋮B\\ \text{thì }\Rightarrow7⋮2n+1\\ \Rightarrow2n+1\inƯ_{\left(7\right)}\\ \text{Mà }Ư_{\left(7\right)}=\left\{\pm1;\pm7\right\}\)
Ta lập bảng giá trị :
| \(2n+1\) | \(-1\) | \(1\) | \(-7\) | \(7\) |
| \(n\) | \(-1\) | \(0\) | \(-4\) | \(3\) |
\(\Rightarrow n\in\left\{-4;-1;0;3\right\}\)
\(\text{Vậy }\text{ để }A⋮B\text{ thì }n\in\left\{-4;-1;0;3\right\}\)
b) Xem lại đề
\(\)
9 tháng 8 2022
a: \(A=n\left(n-1\right)\left(n+1\right)\cdot n\)
TH1: n=2k
n(n-1)(n+1) chia hết cho 6 với mọi n
=>A chia hết cho 12
TH2: n=2k+1
\(A=\left(2k+1\right)\cdot\left(2k+1\right)\cdot2k\cdot\left(2k+2\right)\)
\(=4k\left(k+1\right)\left(2k+1\right)\left(2k+1\right)⋮4\)
mà 2k(2k+1)(2k+2) chia hết cho 6
nen A chia hết cho 12
d: Vì 5 là số nguyên tố nên \(n^5-n⋮5\left(1\right)\)
\(A=n^5-n=n\left(n^4-1\right)\)
\(=n\left(n-1\right)\left(n+1\right)\left(n^2+1\right)⋮6\left(2\right)\)
Từ (1) và (2) suy ra A chia hết cho 30
DH
30 tháng 3 2020
\(2a,2x^3+x^2-6x\)
\(=x\left(2x^2+x-6\right)\)
\(=x\left[2x\left(x+2\right)-3\left(x+2\right)\right]\)
\(=x\left(2x-3\right)\left(x+2\right)\)
\(b,3x^3-4x^2-3x+4\)
\(=x^2\left(3x-4\right)-\left(3x-4\right)\)
\(=\left(3x-4\right)\left(x^2-1\right)\)
\(=\left(3x-4\right)\left(x-1\right)\left(x+1\right)\)
\(c,x^2-4xy+4y^2-xz+2yz\)
\(=x^2-4xy+\left(2y\right)^2-xz+2yz\)
\(=\left(x-y\right)^2-xz+2yz\)
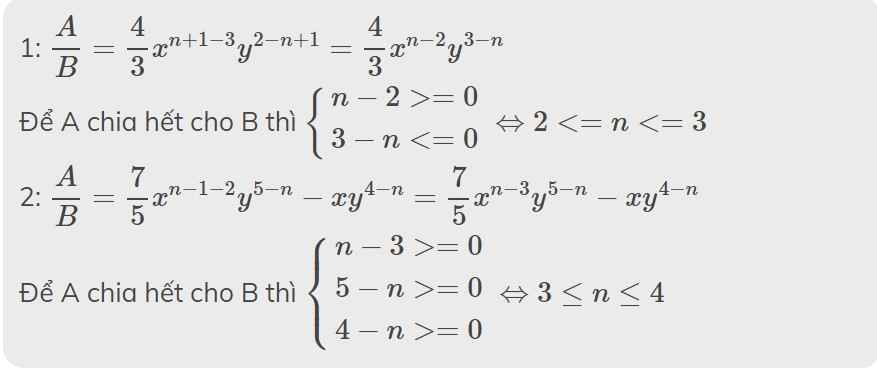
Để am \(⋮\)an ( m \(\ge\)n ; n \(\ne\)0 )
TL :
Để am chia hết cho an thì a phải khác 0 và m phải lớn hơn hoặc bằng n
Chúc bn hok tốt ~