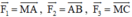Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


6.
ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1}\left(x^2-4x+1-m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\f\left(x\right)=x^2-4x+1-m=0\left(1\right)\end{matrix}\right.\)
a.
Pt có 3 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb lớn hơn 1 hay \(1< x_1< x_2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(1-m\right)>0\\f\left(1\right)>0\\\dfrac{x_1+x_2}{2}>1\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-3\\1-4+1-m>0\\\dfrac{4}{2}>1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-3\\m< -2\end{matrix}\right.\)
\(\Rightarrow-3< m< -2\)
b.
Pt có đúng 2 nghiệm pb khi (1) có 2 nghiệm pb thỏa mãn \(x_1< 1< x_2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=3+m>0\\f\left(1\right)=-2-m< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-3\\m>-2\end{matrix}\right.\)
\(\Rightarrow m>-2\)
7.
\(\sqrt{x^2-3x+m}=4-2x\)
\(\Leftrightarrow\left\{{}\begin{matrix}4-2x\ge0\\x^2-3x+m=\left(4-2x\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le2\\3x^2-13x+16-m=0\left(1\right)\end{matrix}\right.\)
a.
Pt có đúng 2 nghiệm pb khi (1) có 2 nghiệm pb thỏa mãn \(x_1< x_2\le2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=13^2-12\left(16-m\right)>0\\f\left(2\right)=2-m\ge0\\\dfrac{x_1+x_2}{2}=\dfrac{13}{6}\le2\left(ktm\right)\end{matrix}\right.\)
Vậy ko tồn tại m thỏa mãn yêu cầu
b.
Pt có nghiệm duy nhất khi (1) có nghiệm kép \(x=-\dfrac{b}{2a}=\dfrac{13}{6}< 2\) (ktm) hoặc có 2 nghiệm pb sao cho \(x_1\le2< x_2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=13^2-12\left(16-m\right)>0\\f\left(2\right)=2-m\le0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>\dfrac{23}{12}\\m\ge2\end{matrix}\right.\)
\(\Rightarrow m\ge2\)

Lời giải:
Để \(A\cap B\neq \varnothing\) thì $2-5m> m+9$
$\Leftrightarrow m< \frac{-7}{6}$

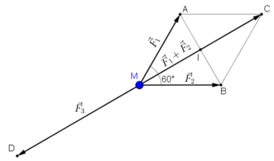
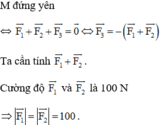
Ta biểu diễn 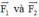 bằng hai vec tơ
bằng hai vec tơ 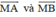 như hình vẽ.
như hình vẽ.
Khi đó 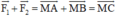 (C là đỉnh còn lại của hình bình hành MACB).
(C là đỉnh còn lại của hình bình hành MACB).
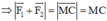
+ Tính MC : Gọi I là trung điểm của AB ⇒ I là trung điểm của MC.
Δ MAB có MA = MB = 100 và góc AMB = 60º nên là tam giác đều
⇒ đường cao 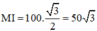
⇒ MC = 2.MI = 100√3.
Vec tơ 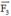 là vec tơ đối của
là vec tơ đối của 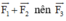 có hướng ngược với
có hướng ngược với 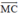 và có cường độ bằng 100√3N.
và có cường độ bằng 100√3N.

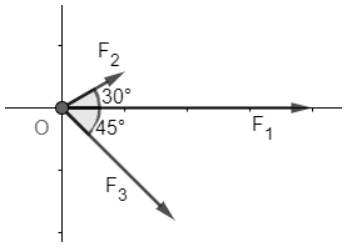
Chọn hệ trục tọa độ Oxy như hình vẽ
Ta có: \(\overrightarrow {{F_1}} = \left( {1500;0} \right)\)
Do \(\;\left( {\overrightarrow {{F_1}} ,{\rm{ }}\overrightarrow {{F_2}} } \right) = 30^\circ \) nên tọa độ của \(\overrightarrow {{F_2}} \)là: \(\overrightarrow {{F_2}} = \left( {600.\cos {{30}^o};600.\sin {{30}^o}} \right) = \left( {300\sqrt 3 ;300} \right)\)
Do \(\left( {\overrightarrow {{F_1}} ,{\rm{ }}\overrightarrow {{F_3}} } \right) = {45^o}\) nên tọa độ của \(\overrightarrow {{F_3}} \)là: \(\overrightarrow {{F_3}} = \left( {800.\cos {{45}^o}; - 800.\sin {{45}^o}} \right) = \left( {400\sqrt 2 ; - 400\sqrt 2 } \right)\)
Do đó, lực \(\overrightarrow F \) tổng hợp các lực tác động lên vật có tọa độ là: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \left( {1500 + 300\sqrt 3 + 400\sqrt 2 ;300 - 400\sqrt 2 } \right)\)
Độ lớn lực tổng hợp \(\overrightarrow F \) tác động lên vật là: \(\left| {\overrightarrow F } \right| = \sqrt {{{\left( {1500 + 300\sqrt 3 + 400\sqrt 2 } \right)}^2} + {{\left( {300 - 400\sqrt 2 } \right)}^2}} \approx 2599\left( N \right)\)

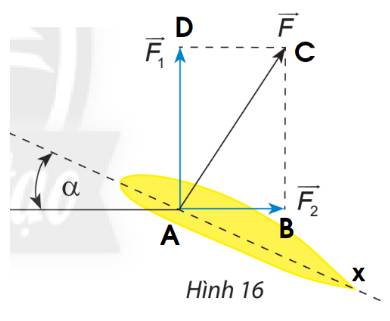
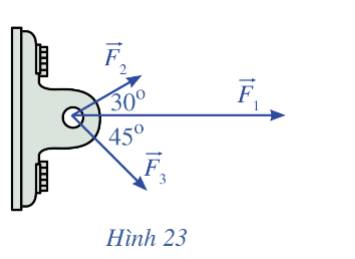
Khi đó các lực \(\overrightarrow F ,\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) lần lượt là \(\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {AB} \)
\(\alpha = \widehat {{\rm{BAx}}} = 30^\circ \) \( \Rightarrow \widehat {CAB} = 60^\circ \)
\(AB = AC.c{\rm{os}}\widehat {CAB} = a.c{\rm{os60}}^\circ {\rm{ = }}\frac{a}{2} \Rightarrow \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {AB} } \right| = \frac{a}{2}\)
\(AD = BC = AC.\sin \widehat {CAB} = a.\sin 60^\circ = \frac{{a\sqrt 3 }}{2} \Rightarrow \left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {AD} } \right| = AD = \frac{{a\sqrt 3 }}{2}\)
Vậy \(\left| {\overrightarrow {{F_1}} } \right| = \frac{{a\sqrt 3 }}{2};\left| {\overrightarrow {{F_2}} } \right| = \frac{a}{2}\)

Tham khảo:
a)
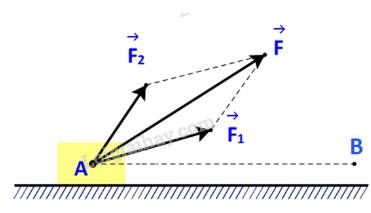
Gọi \(A,{A_1},{A_2}\) lần lượt là công sinh bởi lực \(\overrightarrow F \), \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).
Ta cần chứng minh: \(A = {A_1} + {A_2}\)
Xét lực \(\overrightarrow F \), công sinh bởi lực \(\overrightarrow F \) là: \(A = \left| {\overrightarrow F } \right|.{\rm{ AB}}.\cos \left( {\overrightarrow F ,\overrightarrow {AB} } \right) = \overrightarrow F .\overrightarrow {AB} \)
Tương tự, ta có: \({A_1} = \overrightarrow {{F_1}} .\overrightarrow {AB} \), \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB} \)
Áp dụng tính chất của tích vô hướng ta có:
\({A_1} + {A_2} = \overrightarrow {{F_1}} .\overrightarrow {AB} + \overrightarrow {{F_2}} .\overrightarrow {AB} = \left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right).\overrightarrow {AB} = \overrightarrow F .\overrightarrow {AB} = A\)
b)
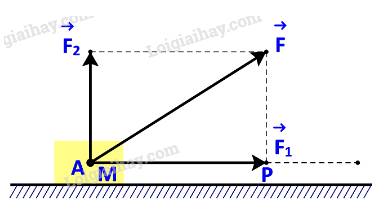
Vì \(\overrightarrow {{F_2}} \)tương ứng vuông góc với phương chuyển động nên \(\overrightarrow {{F_2}} \bot \overrightarrow {AB} \)
Do đó: công sinh bởi lực \(\overrightarrow {{F_2}} \) là: \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB} = 0\)
Mà \(A = {A_1} + {A_2}\)
\( \Rightarrow A = {A_1}\)
Vậy công sinh bởi lực \(\overrightarrow F \) bằng công sinh bởi lực \(\overrightarrow {{F_1}} \).

Tham khảo:
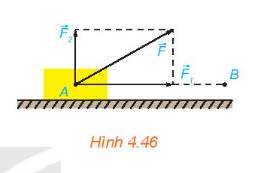
Dựng hình bình hành ABCD với hai cạnh là hai vectơ \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) như hình vẽ
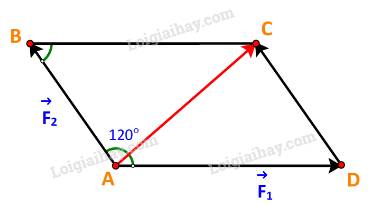
Ta có:
\(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {AD} + \overrightarrow {AB} = \overrightarrow {AC} \Rightarrow \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {AC} } \right| = AC\)
Xét \(\Delta ABC\) ta có:
\(BC = AD = \left| {\overrightarrow {{F_1}} } \right| = 3\;,AB = \;\left| {\overrightarrow {{F_2}} } \right| = 2\;.\)
\(\widehat {ABC} = {180^o} - \widehat {BAD} = {180^o} - {120^o} = {60^o}\)
Theo định lí cosin ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos \widehat {ABC}\\ \Leftrightarrow A{C^2} = {2^2} + {3^2} - 2.2.3.\cos {60^o}\\ \Leftrightarrow A{C^2} = 7\\ \Leftrightarrow AC = \sqrt {7} \end{array}\)
Vậy \(\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \sqrt {7} \)
 GIÚP TUII VỚIIII! CẢM ƠN NHEEEEE
GIÚP TUII VỚIIII! CẢM ƠN NHEEEEE